5/6. В рассмотренных до сих пор случаях равновесие или устойчивость исследовались только для некоторого выбранного состояния или состояний. Ничего не говорилось и не подразумевалось относительно поведения в соседних состояниях.
Возьмем элементарные примеры равновесия: куб, покоящийся на своей грани; бильярдный шар на столе; конус, точно уравновешенный на вершине. Все они обнаруживают некоторое состояние равновесия. Однако равновесие конуса, очевидно, отличается, и существенным образом, от равновесия куба. Различие это обнаруживается, как только эти две системы смещаются внешним возмущающим воздействием из состояния равновесия в какое-нибудь соседнее состояние. Как должно в общем виде представляться это смещение и его результат?
<Возмущение> есть просто то, что смещает, что передвигает систему из одного состояния в другое. Поэтому, определяемое точно, оно должно быть представлено преобразованием, операндами которого служат состояния системы. Предположим теперь, что наша динамическая система содержит преобразование T, что а есть состояние равновесия для Т и что D есть данный оператор смещения. На обычном языке мы говорим: <Сместим систему из ее состояния равновесия, предоставим ей некоторое время следовать ее собственным законам и посмотрим, вернется ли она в то же самое состояние или нет>. В алгебраической форме мы скажем: <Возьмем состояние равновесия а, сместим систему в состояние D(а), а затем найдем
и т. д. и отметим, будет ли эта последовательность состояний иметь окончание а, а, а... или нет>. Говоря короче, состояние равновесия а в системе с преобразованием Т устойчиво относительно смещения D тогда и только тогда, когда .
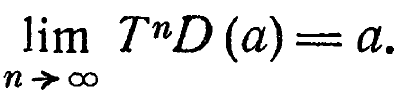
Проверим эту формулировку на трех упомянутых примерах. В случае куба начальное состояние а соответствует наклону в 0°. Оператор D смещает куб, скажем, до 5°, а Т в конце концов возвращает его обратно к 0°, В случае с конусом (имеющим, скажем, преобразование U) D может быть тем же самым смещением, но, конечно, предел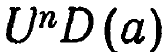
, каков бы этот предел ни был, не есть наклон в 0°,; равновесие неустойчиво. Что касается бильярдного шара в положении а, то законы динамики не вернут его в а после перемещения, так что, по данному определению, шар неустойчив. Однако он имеет ту особенность, что пределом здесь является D(а); таким образом, шар сохраняет перемещение, ни уничтожая, ни увеличивая его. Это случай безразличного равновесия.
(Заметим, что исследовать, как ведет себя система после смещения из а, имеет смысл только в том случае, когда а есть состояние равновесия.),
Упр. 1. Устойчиво ли относительно возмущения D состояние равно- весия с при преобразовании T, если Т и D имеют следующий вид:
| T: |  |
a |
b |
c |
d |
e |
c |
d |
c |
a |
e |
Упр. 2. (Продолжение.) Устойчиво ли состояние равновесия е?
Упр. 3. Область, состоящая из множества состояний b, с и d, устойчива относительно преобразования U:
| U: | |
a |
b |
c |
d |
e |
f |
d |
c |
b |
b |
c |
a |
E: |
b |
e |
f |
f |
f |
d |
Каков будет результат возмущения E, сопровождаемого повторным применением U? (Указание: рассмотрите все три возможности.)