5/4. Цикл, к понятию состояния равновесия близко понятие цикла. Циклом называется такая последовательность состояний, что повторное применение преобразования заставляет представляющую точку пробегать повторно эту последовательность. Так, если Т имеет вид

T:		a	b	c	d	e	f	g	h
		c	h	b	h	a	c	c	g

то, начав с а, Т породит траекторию a c b h g c b h g c b... и представляющая точка будет повторно описывать цикл

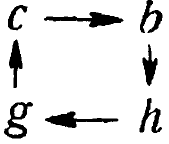
Упр. 1. Напишите преобразование, содержащее два различных цикла и три состояния равновесия.

Упр. 2. (Продолжение.) Начертите его кинематический график.

Упр. 3. Может ли состояние равновесия встретиться в цикле?

Упр. 4. Может ли абсолютная система иметь больше циклов, чем бассейнов?

Упр. 5. Может ли один бассейн содержать два цикла? 1

*Упр. 6. Имеет ли цикл система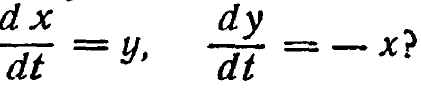   

Упр. 7. Если замкнутое однозначное преобразование имеет конечное число состояний, то может ли траектория кончиться иначе, чем состоянием равновесия или циклом?

1 См. подстрочное примечание на стр. 30. - Прим. ред.