4/2. Мы можем теперь рассмотреть алгебраический способ представления преобразователя.
Три преобразования

можно, очевидно, записать более компактно в виде:

и это показывает нам, как поступить. Следует отметить, что в этом выражении отношения n и a к преобразователю совершенно различны, и это различие никоим образом нельзя терять из виду. Здесь n - операнд, он изменяется преобразованием; то, что это операнд, показывает наличие n'. Но а - параметр; он определяет, какое преобразование должно применяться к n.

Следовательно, значение а должно быть установлено прежде, чем может быть найдено изменение n.

Когда выражения в каноническом представлении станут более сложными, различать переменную и параметр можно, помня, что символы, представляющие операндь, в той или иной форме появятся на левой стороне равенства, как, например, х' или 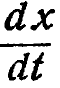; ибо преобразование должно показать, во что они превратятся. Так что все выражения, встречающиеся справа, но не слева, должны быть параметрами. Приводимые ниже примеры пояснят это.

Упр. 1. Какие три преобразования получатся, если задать значения - 1, 0 и +1 параметру ? в , где

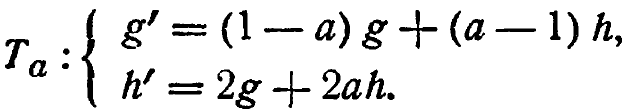
Упр. 2. Какие два преобразования получатся, если параметр а будет принимать значения 0 или 1 в S?

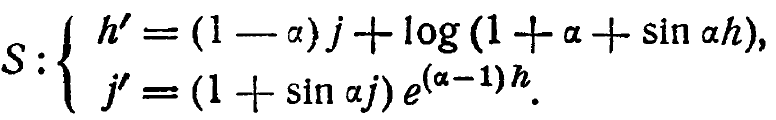
Упр. 3. Преобразователь , в котором аил могут принимать только целые положительные значения, начинает работу с n = 10. (I) Какое значение должно иметь а, чтобы, несмотря на повторные преобразования, n оставалось в 10? (II) Какое значение должно сохранять а, чтобы n изменялось шагами по 4 за один раз (10, 14, 18, ...)? (III) Какие значения а, выбираемые заново при каждом шаге, заставят n пройти ряд 10, 11, 15, 16, 20, 21, 25, 26, .... в котором разность составляет либо 1, либо 4? (IV) Какие зна-. чения а заставят n продвинуться шагами по 1 до 100, а затем одним скачком до 200?

Упр. 4. Пусть преобразователь имеет n операндов, и пусть параметр может принимать также n значений. Будем говорить, что преобразователь дает триединое соответствие между значениями операнда, образа и параметра, если: (1) для данного значения параметра преобразование, осуществляемое преобразователем, является взаимно однозначным; (2) для данного операнда соответствие между значением параметра и образом также является взаимно однозначным. Таков, например, преобразователь

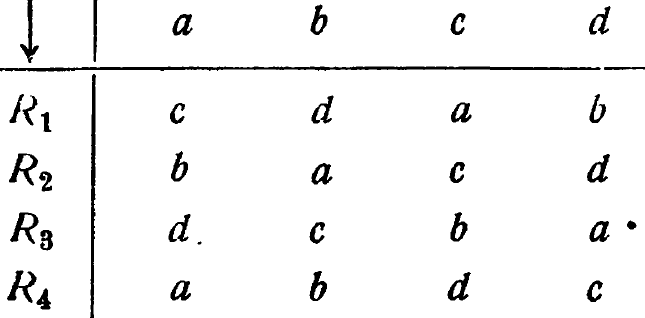
Покажите, что образы должны составить латинский квадрат, т. е. такой квадрат, в котором каждая строка (и каждый столбец) содержит каждый образ один и только один раз.

Упр. 5. Система с одной переменной V ведет себя согласно правилу

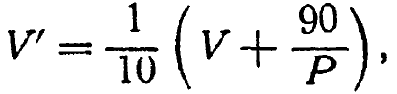
где Р - параметр. Задайте Р некоторое значение например 10, и найдите предел, к которому стремится V при неограниченном повторении преобразования; назовите этот предел . Затем задайте Р другое значение , например 3, и найдите соответствующий предел . Найдя несколько таких пар значений (Р и предельное значение V), посмотрите, не связаны ли они каким-либо законом. Не ведет ли себя V как объем газа под давлением Р?

Упр. 6. Какое преобразование, имеющее параметр а, даст для n три ряда значений:

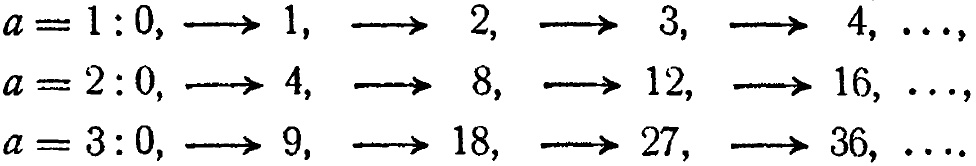
(Указание: испробуйте несколько подходящих выражений, таких как n' = n + а, и т. д.)

Упр. 7. Если n' = n + 3а, то определяет ли значение а величину скачка n при каждом шаге?