4/3. Когда выражение для преобразователя содержит более чем один параметр, число разnичных преобразований может равняться числу возможных комбинаций значений параметров (ибо каждая комбинация может определять отдельное преобразование), но не может превышать его.

Упр. 1. Найдите все преобразования в преобразователе ,если а может принимать значения 0, 1 или 2, а b - значения 0 или 1 и если

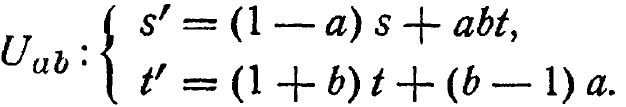
Сколько преобразований содержит это множество?

Упр. 2. (Продолжение.) Если вектор (а, b) может принимать только значения (0,1), (1,1) и (2,0), то сколько преобразований содержит данный преобразователь?

Упр. 3. Преобразователь с переменными р, q начинает работу с (3, 5). Какие значения должны иметь параметры а и д, чтобы (р, q) передвинулось за один шаг в (4, 6). (Указание: выражение для может рассматриваться как система совместных уравнений.)

Упр. 4. (Продолжение.) Найдите затем значение (a, b), которое передвинет систему за один шаг обратно из (4, 6) в (3, 5).

Упр. 5. Преобразователь n' = abn имеет параметры а и b, каждый из которых может принимать значения 0, 1 или 2. Сколько здесь различных преобразований? (Такие неразличимые случаи называются <вырожденными>; правило, приведенное в начале этого параграфа, относится к максимальному числу возможных преобразований; но это максимальное число не всегда достигается.)