4/1. В предыдущей главе мы исследовали отношение между преобразованием и машиной, рассматривая последнюю как нечто единое. Теперь мы попытаемся найти в области преобразований эквивалент присущей каждой обычной машине способности находиться в разnичных условиях и в зависимости от этого изменять свое по ведение, подобно подъемному крану, управляемому водителем, или мышце, управляемой нервом. Для этого необходимо правильно понять, что подразумевается под <параметром>.
До сих пор каждое преобразование рассматривалось само по себе; теперь же мы должны включить в наше рассмотрение отношение между преобразованиями. Опыт показал, что для этого достаточно воспользоваться тем же самым методом, что в 2/3. В самом деле, изменение преобразования А в преобразование В есть не что иное, как переход (согласно 2/3, элементом преобразования может быть все, что поддается ясному определению; поэтому нет никакой причины, чтобы элементы сами не были преобразованиями). Так, если , 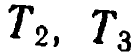- три преобразования, то нет никакой причины, почему бы не определить преобразование

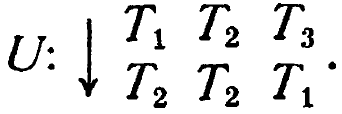
Во избежание путаницы необходимо только не смешивать изменений, вызываемых преобразованием , с изменениями, вызываемыми преобразованием U; любым подходящим в данном конкретном случае способом эти два множества изменений должны мысленно различаться.
Вот обыденный пример преобразования такого же рода, как U. У мальчика имеется игрушечная машина ,построенная из частей, которые можно менять местами. Эту машину он затем разбирает, чтобы сделать новую игрушечную машину 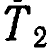. [В этом случае изменения, происходящие, когда машина n переходит от одного состояния к другому (т. е. когда <работает>), ясно отличаются от изменений, происходящих, когда машина превращается в машину ]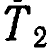

Изменения преобразования в преобразование могут быть, вообще говоря, совершенно произвольными. Нас, однако, будет занимать главным образом тот случай, когда несколько преобразований действуют на одно и то же множество операндов. Так, при четырех общих операндах а, b, с и d можно рассмотреть три преобразования :

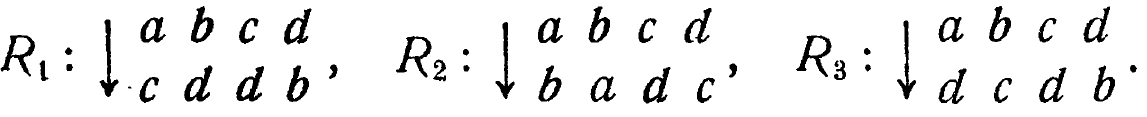
Более компактно их можно записать в виде

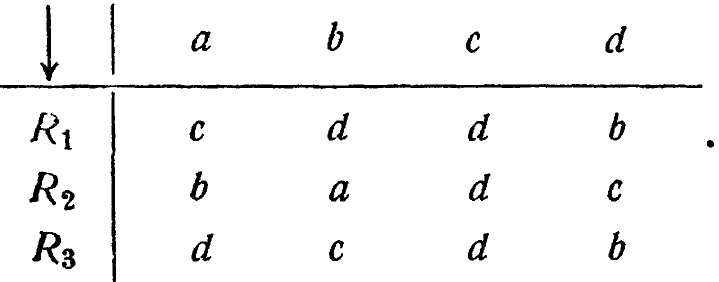
Такую форму записи мы будем использовать как стандартную. (В этой главе мы по-прежнему ограничиваемся рассмотрением лишь замкнутых и однозначных преобразований.) Отдельное преобразование соответствует машине с характерным для нее способом поведения ( 3/1); поэтому совокупность трех преобразований 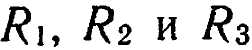, воплощенная в одном и том же физическом теле, должна соответствовать машине с тремя способами поведения. Может ли машина иметь три способа поведения?

Может, так как условия ее работы могут меняться. Многие машины имеют переключатель или рычаг, который можно установить в любом из трех положений, определяя тем самым, какой из трех способов поведения будет иметь место. Так, если буквы a, b, с, d обозначают состояния машины и если соответствует положению 1 такого переключателя, а 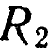соответствует положению 2 переключателя, то изменение индекса буквы R с 1 на 2 соответствует переводу переключателя из положения 1 в положение 2, а это соответствует переходу машины от одного способа поведения к другому.

Мы видим, что слово <изменение> в применении к такой машине может означать две совершенно различные вещи. Существует изменение состояния в состояние, скажем а в b, которое относится к поведению машины и управляется ее собственной внутренней природой; и существует изменение преобразования в преобразование, скажем в 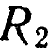, которое представляет собой изменение способа поведения машины и происходит по воле экспериментатора или под действием какого-либо другого внешнего фактора. Это различие носит принципиальный характер, и его ни в коем случае нельзя упускать из виду.

Индекс при R или любой другой символ, значение которого определяет, какое преобразование должно применяться к основным состояниям, будет называться параметром. Если параметр является числовым, то его следует тщательно отличать от любых чисел, которые могут быть использованы для определения операндов как векторов.

Реальная машина, поведение которой может быть представлено таким множеством замкнутых однозначных преобразований, будет называться преобразователем, или машиной со входом (в зависимости от удобства в контексте). Это множество преобразований есть ее каноническое представление. Параметр как нечто, способное изменяться, есть ее вход.

Упр. 1. Пусть S есть преобразование

    
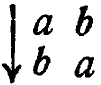
Сколько других замкнутых и однозначных преобразований можно достроить для этих же двух операндов?

Упр. 2. Начертите кинематические графики преобразовани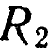й , , и 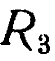(см. выше). Изменится ли график при изменении значения параметра?

Упр. 3. R (см. выше) есть представляющая точка начинает движение в с и делает два шага [до ], затем, когда представляющая точка находится в этом новом состоянии, преобразование изменяется в 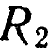и точка делает еще два шага. Где она окажется?

Упр. 4. Найдите последовательность преобразований R, которая переместила бы представляющую точку: (I) от d к а; (II) от d к а.

Упр. 5. Какое изменение в преобразовании соответствует фиксации одной из переменных в машине? Какое преобразование получится, если в системе
х' = - х + 2у,
y' = х - у
переменную х закрепить в значении 4?

Упр. 6. Постройте подходящую таблицу преобразований, на которые действует параметр, и покажите на ее примере, что параметр, даже если он присутствует, может фактически не оказывать никакого воздействия на преобразование.