6/10. В предыдущем параграфе показано, что две машины изоморфны, если простым переименованием можно сделать одну тождественной другой. Однако, как мы сейчас увидим, это <переименование> может иметь различную степень сложности.

Система, заданная только состояниями, как в предыдущем параграфе, не содержит непосредственных ссылок на части или переменные. В этом случае <переименование> может означать лишь <переименование состояний>. Однако в системе с частями или переменными могут быть переименованы и переменные, а это далеко не одно и то же. Переименование переменных в конечном счете есть переименование состояний, но подчиненное значительным ограничениям разнообразия ( 7/8), тогда как переименование состояний может быть сколь угодно произвольным. Таким образом, переименование состояний является более общим, чем переименование переменных.

Например, предположим, что система имеет девять состояний; произвольное переименование восьми из них нисколько не ограничивает выбор названия, которое должно быть дано девятому. Теперь предположим, что система содержит две переменные, каждая из которых может принимать три значения: х1, х2, х3 и y1, y2, y3- Всего возможно девять состояний, два из которых суть (х2, у3) и (х3, y1). Предположим, что переменные системы переименованы следующим образом:

Если теперь (х2, y3) преобразуется в какое-то состояние (, ), а (х3, y1) преобразуется в 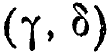, то, во избежание противоречий, состояние (х2, y1) должно переходить в 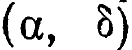. (Начертите фазовые пространства и укажите соответствующие значения на осях- .) Таким образом, в рассматриваемом случае девять состояний не могут быть преобразованы произвольно и независимо.

Переименование переменных оставляет меньше простора для изменения, чем переименование состояний.

Вследствие этого некоторые черты, уничтожаемые при переименовании состояний, сохраняются при переименовании переменных; в частности, так обстоит дело с диаграммой непосредственных воздействий.

Система, описываемая состояниями, не может, конечно, иметь диаграмму непосредственных воздействий, ибо фактически у нее только одна переменная. Напротив, система с переменными имеет диаграмму непосредственных воздействий. Фазовое пространство теперь имеет оси; и легко видеть, после немногих проб, что взаимно однозначное преобразование, переименовывающее переменные, изменяет диаграмму непосредственных воздействий по типу изменения <пуговиц и нитей> ( 2/17), превращая, например, А в В:

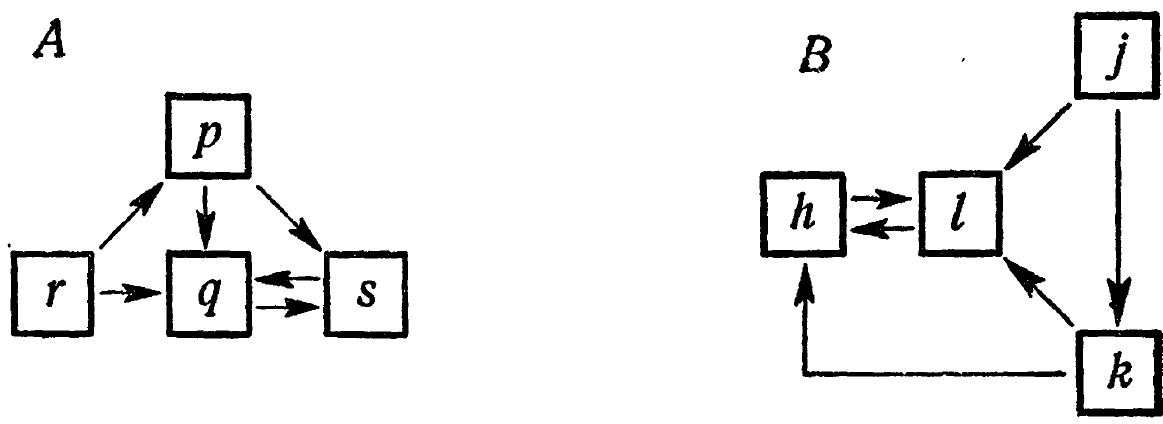
` Упр. 1. (Продолжение упр. 6/9/4.) Сравните диаграммы непосредственных воздействий А и В.

Упр. 2. Отметьте, какие из следующих свойств системы изменяются при переименовании ее состояний, а какие нет: (I) число бассейнов в фазовом пространстве; (II) приводимость системы; (III) число ее состояний равновесия; (IV) наличие обратной связи; (V) число циклов в ее фазовом пространстве.

Упр. 3. (Продолжение.) Как отразится на этих свойствах переименование переменных?