ГОМОМОРФНЫЕ МАШИНЫ 6/12. Данное выше определение изоморфизма определяет <равенство> в самом строгом смысле. Согласно этому определению, две машины (или два <черных ящика>) <равны> только в том случае, когда они столь схожи, что невозможно обнаружить случайную замену одной из них на другую, по крайней мере любым способом проверки их поведения.

Существуют, однако, и меньшие степени сходства. Так, два маятника, один из которых отбивает секунды, а другой - полусекунды, очевидно, сходны, хотя и не изоморфны в строгом смысле слова. Об их сходстве говорит тот факт, что они будут изоморфны при использовании для них отдельных шкал времени, значения одной из которых равны половине значений другой.
Две машины могут быть также связаны <гомоморфизмом>. Это имеет место, когда однозначное лишь в одну сторону преобразование, приложенное к более сложной машине, может свести ее к форме, которая будет изоморфна более простой машине. Так, две машины М и N

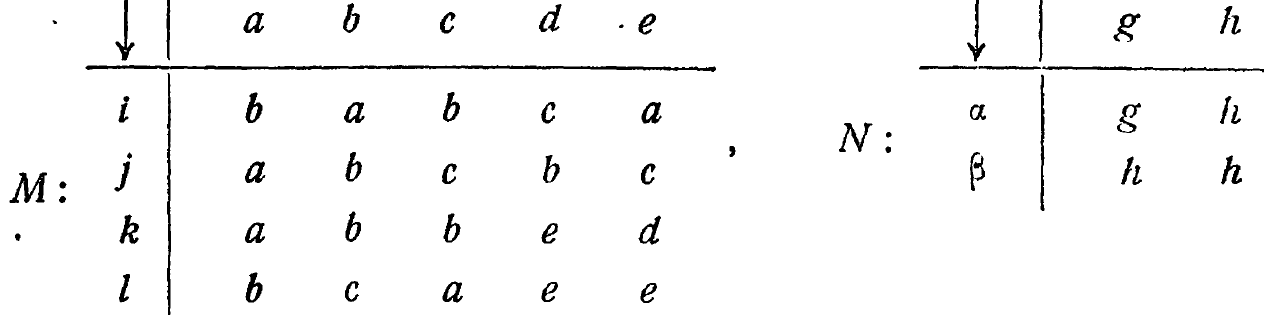
могут показаться на первый взгляд мало в чем сходными. Однако сходство между ними существует, и глубокое. (Читателю будет очень полезно, прежде чем читать дальше, попытаться обнаружить - хотя бы смутно, - в чем заключается это сходство. Обратите внимание на особенность таблицы N, в которой три элемента одинаковы, а один элемент отличается от других. Можно ли обнаружить что-либо подобное в таблице М, если разбить ее на квадраты?)

Преобразуем М посредством однозначного лишь в одну сторону преобразования Т

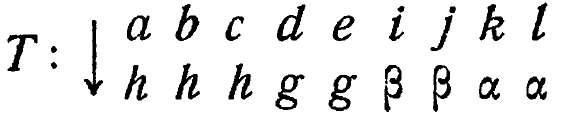
(которое однозначно, но не взаимно однозначно, как в 6/9) и получим

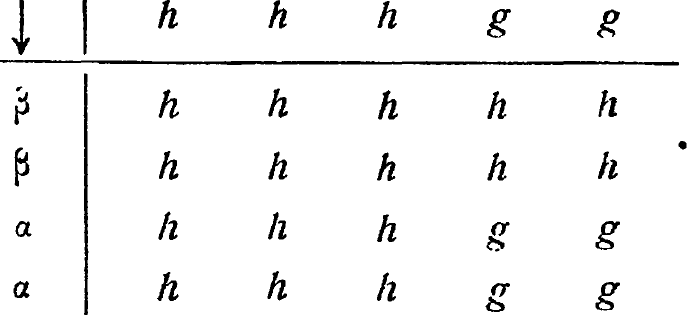
Мы увидим,что повторения не противоречат друг другу, а потому таблицу можно записать в виде

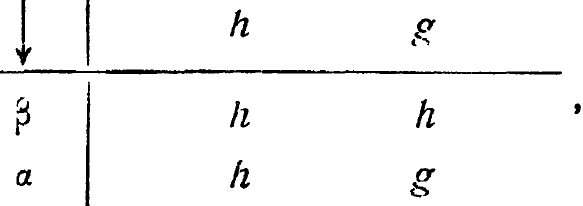
что изоморфно с N.

Исследование М покажет теперь, в чем заключается ее сходство с N. Внутри М переходы происходят по блокам; так, а, b и с всегда переходят только в а, или 6, или с. А блоки в М испытывают те же переходы, что и состояния в N. Таким образом, N эквивалентно упрощенному варианту М.

Это соотношение между машинами М и N можно обнаружить и по-другому.

Предположим сначала, что обе машины рассматривает некто, способный различать все пять состояний М он скажет просто, что М отлично от N (т. е. не изоморфно с N) и более сложно, чем N. Предположим, что машины рассматривает также наблюдатель с меньшей способностью различения, который не может различить а, b и с и смешивает их в одно состояние, скажем в А. Равным образом он смешивает d и е, скажем, в В, i и j - в Г, a k и l - в . Этот новый наблюдатель, видя упрощенный вариант M, скажет, что М изоморфно с N. Таким образом, две машины гомоморфны, если они становятся одинаковыми при упрощении одной из них, т. е. при наблюдении ее с неполным различением состояний.

Формально мы скажем: если две машины находятся в таком отношении друг к другу, что некоторое однозначное лишь в одну сторону преобразование, приложенное к одной из них, даст машину, изоморфную другой машине, то эта вторая (более простая) машина есть гомоморфный образ первой машины.

Упр. Является ли изоморфизм лишь крайним случаем гомоморфизма? Задача. Какие еще типы гомоморфизма существуют между машинами?