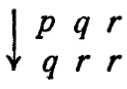6/16. Модели. Теперь мы можем яснее видеть, что понимается под <моделью>.

Об этом уже говорилось в 6/8, где был установлен изоморфизм трех рассмотренных нами систем и вытекающая отсюда способность их изображать друг друга. Указанный вопрос имеет немалое значение для тех, кто работает с биологическими системами, ибо во многих случаях использование модели может принести пользу: модель помогает исследователю думать о данном предмете либо действует в качестве аналогового вычислительного устройства.

Модель редко бывает изоморфна биологической системе; обычно она лишь гомоморфна ей. Но и сама модель редко рассматривается во всех своих практических деталях: обычно лишь некоторые .аспекты модели соотносятся с биологической системой. Например, оловянная мышь может быть удовлетворительной моделью живой мыши, если только не обращать внимания на то, что одна состоит из олова, а другая - из белка. Таким образом, обычно получается, что две системы - биологическая и модель - связаны между собой так, что некоторый гомоморфный образ одной из них изоморфен некоторому гомоморфному образу другой. (Это отношение симметрично, так что каждая из обеих систем может быть названа <моделью> другой.) Чем выше расположены гомоморфные образы в структурах своих систем, тем лучше и реалистичнее будет модель.

Здесь наше введение в кибернетику должно закончить рассмотрение гомоморфизмов. Было сказано достаточно, чтобы показать основные положения этого раздела и наметить линии его развития. Но само это развитие принадлежит будущему.

Упр. 1. Что это за случай, когда изоморфны самые верхние элементы двух структур?

Упр. 2. До какой степени Гибралтарская скала является моделью мозга?

Упр. 3. Какие модели для системы из упр. 6/13/2 может дать машина