6/5. Абсолютность. Получив достаточно длинные записи, экспериментатор приступает к поискам закономерностей в поведении, к поискам повторяемости в поведении ( 7/19). Например, в упр. 6/3/1 он может заметить, что за j всегда следует либо f, либо f, следовательно, хотя переход от а неоднозначен, переход от j однозначен.

Итак, экспериментатор исследует записи. Обычно первая его задача - установить, является ли <ящик> абсолютным при данном входном состоянии. Для этого экспериментатор должен:

(I)     выписать все переходы, следующие за входным состоянием , и рассортировать их , на переходы от g, переходы от h и т. д. по всем выходным состояниям;

(II)    сделать то же самое для входа ;

(III)   и т. д. по всем наблюдаемым входным состояниям.

Иными словами, он старается найти такое множество преобразований, как в 4/1, и исследует полученное им множество, чтобы установить, однозначны ли эти преобразования.

Так, пусть рассматривается приведенный выше протокол (упр. 6/3/1). Если записать каждый из 16 образов, то получится таблица

	f	g	h	j
	fff	j	jjj	ff
	hhh	.	hh	ff

(Переход от g при входе не наблюдался.) Все буквы в каждой клетке одинаковы, так что таблица упрощается:

	f	g	h	j
	f	j	j	f
	h	.	h	f

отсюда вывод, что на протяжении всего протокола наблюдалось это замкнутое однозначное преобразование.

Таким образом, прямым перекодированием протокола экспериментатор может показать, что данное поведение машиноподобно, и может вывести его каноническое представление.

Следует отметить, что он вывел каноническое представление из прямого наблюдения над действительным поведением <ящика>. Экспериментатор не опирался ни на какое <заимствованное> знание. Чего бы он ни ожидал и как бы он ни был уверен в своих ожиданиях, окончательный вывод зависит только от того, что действительно случилось. Таким образом, в любом конфликте между тем, чего ожидал экспериментатор или другие лица, и тем, что было обнаружено, эти эмпирические результаты являются решающими, составляя проявление природы <ящика>.

Если система не детерминированна, т. е. преобразование не однозначно, экспериментатор может пойти по одному из двух следующих путей.

Первый путь - изменить множество входов и выходов, приняв во внимание большее количество переменных, а затем посмотреть, не является ли новая система (эквивалентная новому <ящику>, см. 3/11) детерминированной. Так, химик может обнаружить, что поведение системы, сначала недетерминированное, становится детерминированным, если принять во внимание присутствие следов хлорида. Значительное число исследований состоит из таких поисков подходящего множества переменных.

Другой путь состоит в том, чтобы отказаться от поисков строгой детерминированности и попытаться отыскать статистическую детерминированность, т. е. детерминированность в среднем и т. д. Если подробности не являются предсказуемыми от шага к шагу, то экспериментатор, собрав обширные записи, разбивает их на большие отрезки и исследует, не являются ли средние значения (или аналогичные статистические характеристики) предсказуемыми от отрезка к отрезку. Он может установить, что записи обнаруживают статистическую детерминированность, соответствующую марковской цепи. (Однако рассмотрение этого случая будет отложено до гл. 9, а до тех пор мы будем заниматься только машинами, детерминированными от шага к шагу.)

Подведем итог: получив протокол, можно испытать систему на детерминированность и (если детерминированность установлена) вывести каноническое представление системы.

Упр. 1. Выведите кинематический график для входа а непосредственно из протокола системы 6/3.

Упр. 2. (Продолжение.) То же для входа .

Упр. 3. Система с одним входным состоянием дает следующую последовательность состояний на выходе:
D G А Н С L H C L H C F C ... .
Абсолютна ли эта система?

Упр. 4. Система имеет две переменные х и у, каждая из которых может принимать значения 0, 1 и 2. Вход может принимать два значения: . Дан протокол:

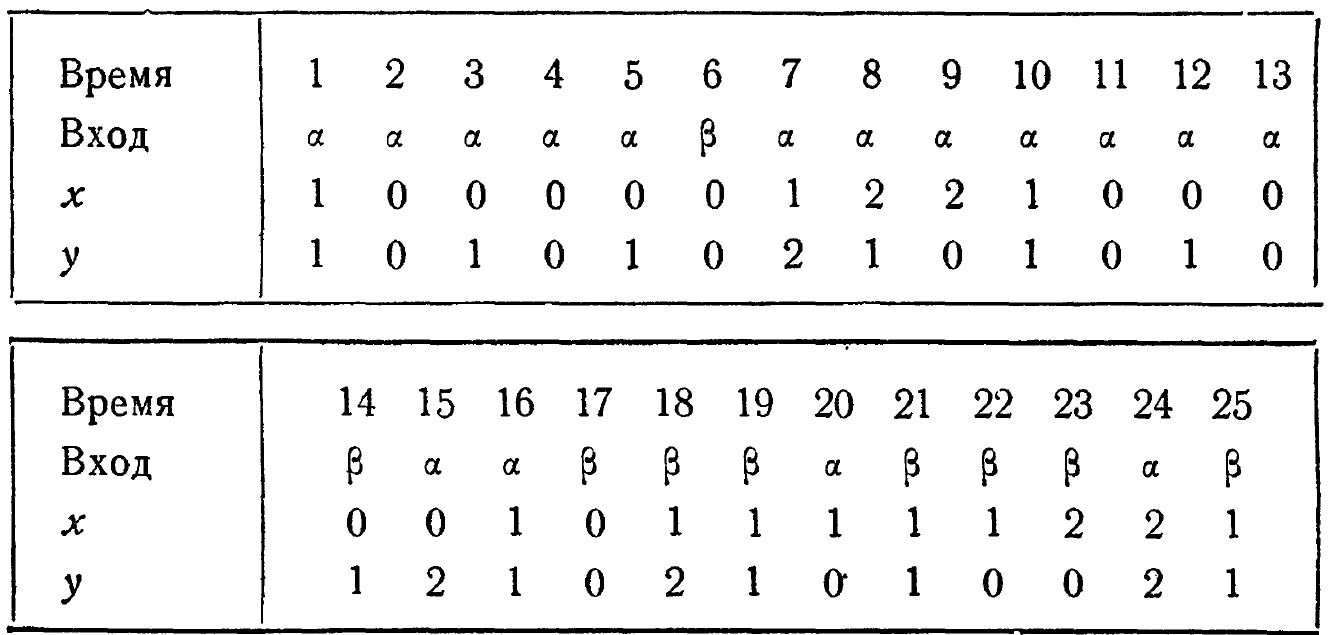
Является ли эта система машиной со входом?

Упр. 5. (Продолжение.) Каково будет ее преобразование при входе ?

Упр. 6. Если машина имеет т входных и n выходных состояний, то каково наименьшее число шагов наблюдения, достаточное для ее полного изучения?

Упр. 7. Два <черных ящика> имеют одинаковый внешний вид, и каждый имеет по одному входу а и одному выходу х, которые являются числовыми переменными. <Ящики> были обозначены знаками I и II, и были найдены их канонические представления:

I) х' = х +1 -

II) x' = (1+ )х - 2 + .

К несчастью, знаки I и II были затем перепутаны, так что теперь неизвестно, какой из них относится к какой формуле. Предложите простейший способ установить их место.