2/8. Из однозначных преобразований особое значение в ряде случаев имеют взаимно однозначные (1) преобразования. Во взаимно однозначном преобразовании все образы отличаются друг от друга. Следовательно, не только каждый операнд дает единственный образ (согласно условию однозначности), но и каждый образ указывает (обратно) на единственный операнд. Таково преобразование

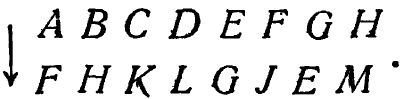
Это пример взаимно однозначного, но не замкнутого преобразования. С другой стороны, преобразование из упр. 2/6/2(е) не является взаимно однозначным, ибо образ <1> не указывает единственного операнда.

Однозначное, но не взаимно однозначное преобразование будет называться однозначным лишь в одну сторону.

1 Однозначность преобразования часто в дальнейшем молчаливо предполагается. Так, например, лишь в предположении однозначности справедливы ответы к упражнениям 5/4/5 и 5/5/3. - Прим. Ред.

Упр, 1. Операнды - десять цифр 0, 1,:,     9;     образ -третий десятичный разряд числа lg (n+ 4). Например, если операндом служит 3, то последовательно находим: 7, lg 7, 0,8451 и 5; следовательно, 35. Является ли это преобразование взаимно однозначным или однозначным лишь в одну сторону? (Указание: найдите последовательно образы для 0, 1 и т. д., употребляя четырехзначные таблицы логарифмов.)