2/15. Обозначения. Способ записи, при котором образ обозначается прибавлением штриха, удобен, если рассматривается только одно преобразование; но если на n может действовать несколько преобразований, то символ n' не указывает, какое из них действовало. Поэтому иногда употребляется другой символ: если n - операнд и применяется преобразование T, то образ обозначается через Т(n). Четыре печатных знака - две буквы и две скобки - изображают одну величину; это обстоятельство может спутать того, кто еще не привык к нему. Выражение Т(n), которое на самом деле является переиначенным n', может быть снова преобразовано, и тогда его следовало бы записать в виде T(T(n)), если запись единообразна; практически внешние скобки обычно опускаются и повторяющиеся Т объединяются, так что n'' пишется как . Приводимые ниже упражнения должны приучить читателя к этому способу записи (ибо изменяется здесь только способ записи).

Упр. 1. Если ?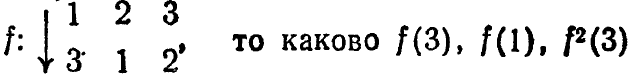

Упр. 2. Выпишите полностью преобразование h для операндов 6. 7, 8, если g(6) =8, g(7) = 7, g(8) =8.

Упр. 3. Выпишите полностью преобразование h для операндов если , .

Упр. 4. Если А (n) есть n + 2, то каково A(15)?

Упр. 5. Если f(n) есть , то каково f(2)?

Упр. 6. Если Т(n) есть 3n, то каково ? (Указание: если вы не уверены в ответе, выпишите Т полностью.)

Упр. 7. Если I есть тождественное преобразование, a t - один из его операндов, то каково I(t)?