ГЛАВА 2. Повторные изменения

2/13. Исключение символов. Если преобразование задано в сокращенной форме, например формулой n' = n' + 1, то результат его двукратного применения можно также найти с помощью описанных методов. Для этого надо записать преобразование заново, показывая все операнды, осуществить его двукратное применение и затем снова сократить запись. Существует, однако, более быстрый метод. Чтобы показать и объяснить его, выпишем полностью преобразование Т : n' = n + 1 для положительных целых чисел, а внизу запишем результаты его двойного применения и поставим общий символ выполненных операций:

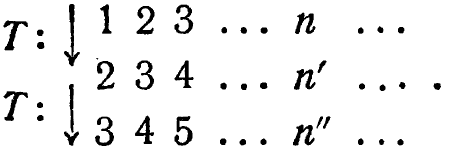
Здесь n" используется как естественный символ для образа от n', так же как n' есть образ от n.
Итак, нам дано, что n' = n+ 1. Так как мы применяем то же самое преобразование снова, то n'' должно быть на 1 больше, чем n'. Следовательно, n" = n' + 1.

Чтобы определить однократное преобразование , нам нужно уравнение, выражающее образ n'' непосредственно через операнд n. Нахождение этого уравнения есть просто вопрос алгебраического исключения символов: из двух уравнений n'' = n' + 1 и n' = n + 1 нужно исключить n'. Подставляя n + 1 вместо n' в первое уравнение, получим (скобки указывают процесс подстановки) n'' = (n + 1) + 1, т. е. n" = n + 2.

Это уравнение задает точную зависимость между операндом (n) и образом (n") при и тем самым определяет . Для унификации обозначений это уравнение можно переписать в виде m' = m + 2. Так выглядит в стандартной записи преобразование, однократное применение которого (отсюда один штрих у m) вызывает те же самые изменения, что и двукратное применение Т (замена n на m означает простую перемену названия во избежание путаницы).

Мы высказали вполне общее правило. Так, если дано преобразование n' = 2n' - 3, то второе применение его даст вторые образы n", связанные с первыми формулой n'' = 2n' - 3. Производя подстановку вместо n' и свободно используя скобки, получим
n'' = 2(2n' - 3) - 3 = 4n - 9.

Следовательно, двукратное применение преобразования n' = 2n' - 3 вызывает те же изменения, что и одно применение преобразования m' = 4m - 9.