ГЛАВА 2. Повторные изменения

2/14. Высшие степени. Высшие степени находятся простым добавлением символов для высших образов (n''' и т. д.) и исключением символов промежуточных образов. Так, найдем преобразование, вызываемое трехкратным применением преобразования n' = 2n' - 3. Выпишем уравнения шаг за шагом:
n' = 2n' - 3,
n'' = 2n' - 3,
n''' = 2n'' - 3.

Возьмем последнее уравнение и, подставив 2n'-3 вместо n'', получим
n''' = 2(2n' -3) -3 = 4n' -9.
Теперь подставим вместо n':
n''' = 4(2n -3) - 9 = 8n -21.

Следовательно, трехкратное применение вызывает те же самые изменения, какие вызвало бы одно применение преобразования m' = 8m - 21. Если первоначальное преобразование было Т, то трехкратное преобразование есть .

Упр. 1. Исключите n' из n'' = Зn' и n' = 3n.
Постройте соответствующее преобразование и проверьте, что два применения преобразования n' = 3n дают тот же результат.

Упр. 2. Исключите а' из а" = а' + 8 и а'= а + 8.

Упр. 3. Исключите а" и а' из а'" = 7a'', а" = 7а', а' = 7а.

Упр. 4. Исключите k' из k" = -3k' + 2, k' = -3k + 2. Проверьте, как в упр. 1.

Упр. 5. Исключите m' из m" = log m', m' = log m.

Упр. 6. Исключите р' из , .

Упр. 7. Найдите преобразования, эквивалентные двукратным применениям (ко всем положительным целым числам, большим 1) преобразований:

.

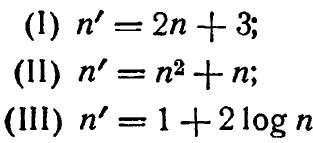Упр. 8. Найдите преобразование, эквивалентное трехкратному применению преобразования n'= -3n-1 к положительным и отрицательным целым числам и нулю. Проверьте, как в упр.1.

Упр. 9. Найдите преобразования, эквивалентные второму, третьему и дальнейшим применениям преобразования n' = 1/(n+1).

(Замечание: здесь используется ряд, открытый Фибоначчи в XII веке: 1, 1, 2, 3, 5, 8, 13,...; в ряде Фибоначчи каждый следующий член равен сумме двух предшествующих:
так, 3 + 5 = 8, 5 + 8 = 13, 8 + 13 = ... и т. д.) (Замечание: здесь используется ряд, открытый Фибоначчи в XII веке: 1, 1, 2, 3, 5, 8, 13, ...; в ряде Фибоначчи каждый следующий член равен сумме двух предшествующих: так, 3 + 5 = 8, 5 + 8=13, 8 + 13 = ... и т. д.)

Упр. 10. Каков результат двукратного применения преобразования n' = 1/n, если операнды суть все положительные рациональные числа (т. е. все дроби)?

Упр. 11. Геометрическое преобразование. Нарисуйте на бумаге отрезок и обозначьте его концы через А и В. Этот отрезок, определяемый длиной и положением, есть операнд. Получите его образ с концами А' и В' следующим преобразованием R: A' есть середина АВ, а В' находится поворотом отрезка А'В вокруг A' на прямой угол против часовой стрелки. Проведите A'B'; затем применяйте R повторно и выясните, как себя будет вести система.

*Упр. 12. (Продолжение.) Если вы знакомы с аналитической геометрией, примите за А точку (0,0) и за В точку (0,1); найдите предельное положение. (Указание: определите окончательную абсциссу точки А как ряд и просуммируйте его;то же проделайте и для ординаты точки А.)