
ГЛАВА 2. Преобразования
2/10. Матричное представление. Все эти преобразования могут быть представлены в единой схеме, ясно показывающей их взаимоотношения (этот метод будет особенно полезен в гл. 9 и дальше).
Выпишем операнды в горизонтальную строку, а возможные образы - в столбец слева вниз, так, чтобы образовать две стороны прямого угла. Пусть нам дано некоторое преобразование. Поставим <+> на пересечении строки и столбца, если операнд, стоящий вверху столбца, преобразуется в элемент, стоящий слева в строке,; в противном случае поставим нуль. Например, преобразование
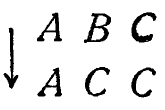
будет иметь вид
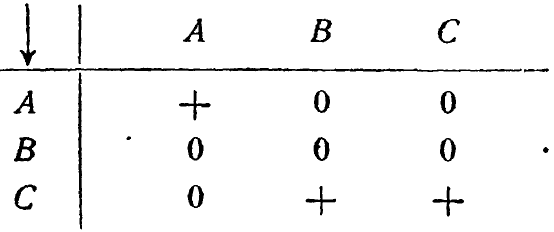
Стрелка в левом верхнем углу указывает направление переходов. Таким образом, каждое преобразование может быть представлено в виде матрицы.
Если преобразование велико, в матрице можно использовать точки; надо только, чтобы их значение не было двусмысленным. Так, возьмем преобразование, при котором n' = n + 2, а операнды суть целые положительные числа начиная с 1. Его матрица может быть представлена в следующем виде:
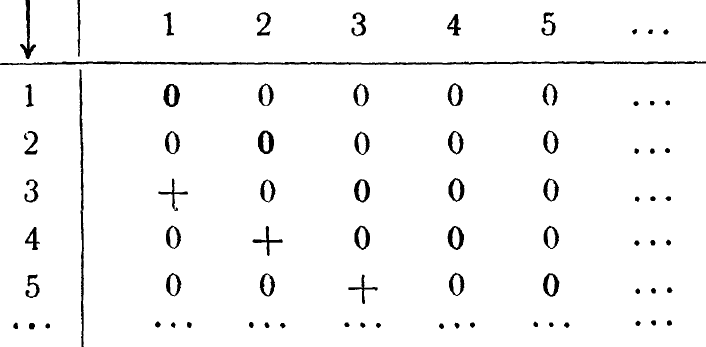
(Символы на главной диагонали, идущей от левого верхнего угла, напечатаны полужирным шрифтом для большей ясности позиционных отношений.)
Упр. 1. Как распределены плюсы в матрице тождественного преобразования?
Упр. 2. Какое из трех указанных преобразований: а) взаимно однозначно; b) однозначно, но не взаимно однозначна; с)однозначно? 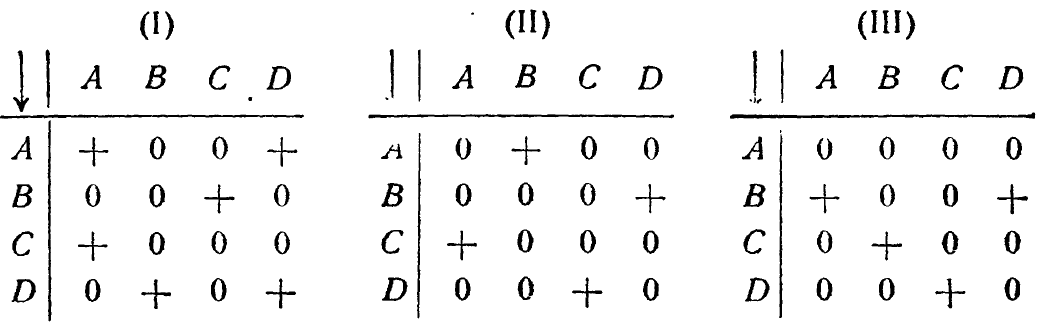
Упр. 3. Может ли замкнутое преобразование иметь матрицу, содержащую: а) строку из одних нулей; b) столбец из нулей?
Упр. 4. Постройте матрицу преобразования n' = 2n с целыми числами в качестве операндов, делая ясным распределение плюсов. Лежат ли они на прямой линии? Начертите график у = 2х; имеют ли эти линии какое-либо сходство?
Упр. 5. Возьмите колоду карт, перетасуйте ее и разложите 16 карт лицевой стороной кверху в квадрат четыре на четыре. В матрицу четыре на четыре ставьте знак +, если на соответствующем месте лежит карта черной масти, и ставьте знак 0, если на соответствующем месте лежит карта красной масти. Проделайте это несколько раз, определяя тип каждого преобразования, как в упр. 2.
Упр. 6. Если имеется два операнда и преобразование замкнуто, то сколько существует различных матриц?
Упр. 7. (Продолжение.) Сколько из них однозначны?
Ответ
2/10: 1. На главной диагонали стоят только +, на остальных местах-нули. 2. а) (II); b) (III); с) (I). 3. а) Да. b) Нет.
4. Распределения одинаковы; одно есть просто отражение другого. 6. 9 1) - 7. 4.
1) Вот эти матрицы:

В оригинале в качестве ответа ошибочно указано число 16. (Такое число действительно получится, если допускать столбцы, целиком заполненные нулями, т. е. "операнды, не имеющие образов"). Прим. ред.
