ГЛАВА 2. Повторные изменения

2/16. Произведение. Как мы только что видели, после применения преобразования Т к операнду n образ T(n) может рассматриваться как новый операнд для Т, что дает образ T(T(n)), обозначенный через . Точно так же Т(n) может стать операндом преобразования U, что даст образ U(T(n)). Так, если имеются преобразования

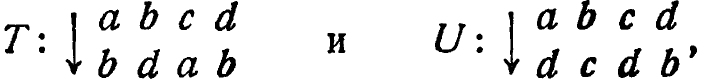
то T(b) есть d, a U(T(b)) есть U(d), т. е. b. Преобразования Т и U, примененные в таком порядке, определяют новое преобразование V, которое легко обнаружить:

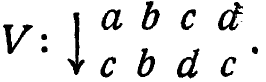
Преобразование V называется произведением, или композицией, преобразований Т и U. Оно дает просто результат последовательного применения Т и U в данном порядке, каждого по одному разу.

Если сначала применяется U, то U(b) в приведенном примере есть с, а Т(с) есть a; отсюда T(U(b)) есть а, т. е. не то же самое, что U(T(b)). Когда U и Т применяются во втором порядке, их произведением служит преобразование

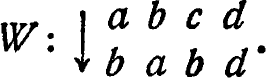
Для удобства V может записываться как UT, a W - как TU. Всегда надо помнить, что изменение порядка в произведении может изменить преобразование.

(Заметим, что произведение V может быть невозможным, т. е. не существовать, если некоторые из образов преобразования Т не являются операндами для U.).

Упр. 1. Выпишите преобразование .

Упр. 2. Выпишите полностью UTU.

Упр. 3. Представьте Т и U посредством матриц, а затем перемножьте эти две матрицы обычным образом (строки на столбцы), принимая, что произведение и сумма знаков + есть +; назовите полученную матрицу . Представьте V матрицей; назовите ее . Сравните и .