2/17. Кинематический график. До сих пор мы изучали каждое преобразование главным образом путем наблюдения за результатом его однократного действия на все его возможные операнды (см., например, 2/3), Другой метод (применимый только к замкнутым преобразованиям) состоит в изучении действия преобразования на отдельный операнд при многих повторных применениях. Этот метод соответствует при изучении динамических систем тому, что систему приводят в некоторое начальное состояние, а затем предоставляют ей без дальнейшего вмешательства проходить серию изменений, определяемых ее внутренней природой. Так, в автоматической телефонной системе мы можем наблюдать все изменения, которые следуют за набором номера; я муравейнике мы можем наблюдать все изменения, которые последуют, если положить поблизости кусочек мяса.

Предположим для определенности, что мы имеем преобразование

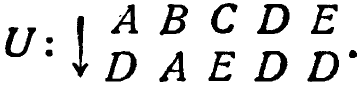
Если U применяется к С, затем к U(C), затем к , затем к и т. д., то образуется ряд С, Е, D, D, D,... и т. д., где D повторяется без конца. Если U применять таким же образом к A, то образуется ряд A, D, D, D,..., где D повторяется опять.

Эти результаты можно изобразить графически, получая тем самым возможность обнаруживать с первого же взгляда соотношения, которые в противном случае могли бы быть обнаружены только после тщательного изучения. Чтобы построить кинематический график преобразования, выписывается множество всех операндов, каждый на любом удобном месте, и затем они соединяются стрелками согласно правилу, что стрелка идет от A к B тогда и только тогда, когда A за один шаг преобразуется в В. Так, U дает кинематический график

(К D можно и не приписывать <возвратную> стрелку, если от этого не возникает никакого недоразумения.)
Если бы график состоял из пуговиц (операндов), связанных нитями (переходами), он мог бы, подобно какой-нибудь сети, принимать различные формы:

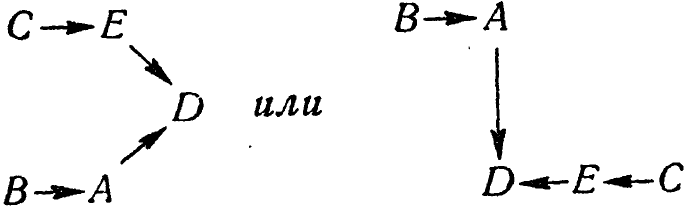
и т. д. Эти различные формы не рассматриваются как различные графики, если только внутренние связи в них тождественны.
Элементы, получаемые при последовательных преобразованиях элемента С посредством U (ряд С, Е, D, D,:),находятся в постоянном очевидном соответствии с состояниями, проходимыми на кинематическом графике точкой, которая начинает движение в С и проходит по одной стрелке за шаг, двигаясь всегда по направлению стрелки. Так как проследить движение точки по линии обычно гораздо легче, чем вычислить U(C), и т. д., особенно при сложном преобразовании, то график часто является самым удобным представлением преобразования в изобразительной форме. Движущаяся точка будет называться представляющей точкой.
Когда преобразование становится более сложным, выступает одна его важная черта. Возьмем, например, преобразование

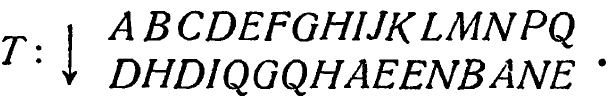
Его кинематический график имеет вид

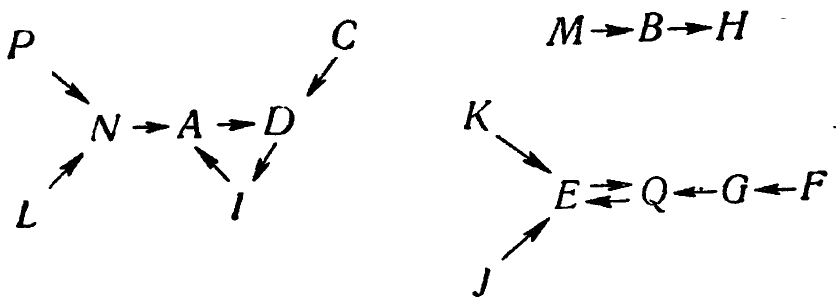
        Начиная, движение из любого состояния и следуя по цепи стрелок, мы можем убедиться, что при повторных преобразованиях представляющая точка приходит всегда либо к некоторому положению, в котором она останавливается, либо к некоторому циклу, в котором циркулирует до бесконечности. Такой график напоминает карту дренажной системы, показывающую, в какой район попадет в конце концов капля воды (т. е. представляющая точка), начавшая свой путь в любом месте. Эти обособленные друг от друга районы называются бассейнами графика. Очевидно, это имеет некоторое отношение к тому, что понимается под <устойчивостью>, к которой мы перейдем в гл. 5.

Упр. 1. Начертите кинематический график преобразований А и В в упр. 2/4/3.

Упр. 2. Как можно с первого взгляда узнать график тождествен- ного преобразования?

Упр. 3. Начертите графики каких-нибудь простых замкнутых и взаимно однозначных преобразований. Что является их отличительным признаком?

Упр. 4. Начертите график преобразования V, в котором n' есть третья десятичная цифра числа lg(n + 20), а операнды - десять цифр 0, 1, .... 9.

Упр. 5. (Продолжение.) По графику V определите сразу, каковы V(8), .

Упр. 6. Если преобразование взаимно однозначно, то могут ли две стрелки приводить в одну точку?

Упр. 7. Если преобразование однозначно лишь в одну сторону, то могут ли две стрелки приводить в одну точку?

Упр. 8. Постройте какие-нибудь замкнутые однозначные преобразования, подобные T, начертите их кинематические графики и отметьте их характерные признаки.

Упр. 9. Если преобразование однозначно, то может ли один бассейн содержать два цикла?