12/8. Теперь мы переходим к рассмотрению более общего класса машин, чем тот, который рассматривался в первой и второй частях. [Логически он должен был бы рассматриваться раньше, но в первых двух частях столько места занимала детерминированная машина (т. е. машина, преобразования которой однозначны), что рассмотрение более общего типа могло бы внести путаницу.] <Машина> есть по существу система, поведение которой является достаточно закономерным или повторяющимся, чтобы мы могли делать определенные предсказания о ее будущих действиях ( 7/19).

Такие предсказания могут иметь различные формы. Для одной машины мы можем предсказать ее следующее состояние; тогда мы говорим, что она <детерминироваванна> и относится к машинам, рассмотренным в части I. Для другой машины мы не сможем предсказать ее следующее состояние, но сможем предсказать, что при многократном повторении тех же условий частоты различных состояний будут иметь определенные значения. Это возможное постоянство частот уже было отмечено в 9/2: Оно является характеристикой цепи Маркова.

Итак, мы можем рассмотреть новый класс абсолютных систем - систем, состояния которых изменяются во времени не в соответствии с однозначным преобразованием,но в соответствии с матрицей переходных вероятностей. Чтобы эта система оставалась одной и той же, значения вероятностей должны быть неизменными. В 2/10 было показано, что однозначное преобразование может задаваться матрицей переходов, в клетках которой стоят 0 и 1 (там для простоты ставились 0 и +). В 9/4 цепь Маркова задавалась аналогичной матрицей, содержащей дроби. Таким образом, детерминированная абсолютная система является особым случаем марковской машины; она является предельной формой марковской машины, в которой все вероятности превратились либо в 0, либо в 1 (ср. 9/3).

"Машина со входом" была множеством абсолютных систем, различающихся параметром. По аналогии марковская машина со входом должна быть множеством марковских машин, определяемых множеством матриц с параметром, значения которого указывают, какая матрица должна использоваться на данном шаге.

Понятие марковской машины является естественным расширением понятия обычной детерминированной машины, рассматривавшейся в части I. Если все вероятности равны 0 или 1, то эти два типа тождественны. Если все вероятности очень близки к 0 или 1, то мы получаем машину, поведение которой почти детерминированно, но которая по временам допускает неожиданные отклонения. По мере того как вероятности все дальше отходят от 0 и 1, поведение машины становится все менее определенным и все более напоминающим по-ведение одного из насекомых из 9/4.

Следует отметить, что это определение, хотя и допускает некоторую неопределенность, в других отношениях остается абсолютно, строгим. Если машина из состояния х переходит в 90% случаев в состояние у и в 10% случаев в состояние г, то эти проценты должны быть постоянными (в том смысле, что с удлинением последовательности относительные частоты должны стремиться к этим процентам и что эти пределы должны оставаться неизменными для всех последовательностей).

Практически это означает, что условия, определяющие процентное соотношение, должны оставаться постоянными.

Нижеследующие упражнения помогут читателю несколько освоиться с понятием марковской машины.

Упр. 1. Маятник метронома постоянно колеблется между двумя крайними состояниями R и L, но, находясь справа (R)., он имеет вероятность в 1% остановиться там. Какова его матрица переходных вероятностей?

Упр. 2. Детерминированная машина а имеет преобразование

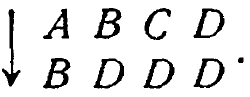
Марковская машина имеет матрицу переходных вероятностей
      А      В      C     D
А      0      0      0      0
В      0,9   0      0      0
С     0      0      0,2   0
D     0,1   1,0   0,8   1,0

Как различается их поведение? (Указание: начертите график а, а затем начертите график р, позволив вероятностям перейти в 0 и 1).

Упр. 3. Марковская машина со входом имеет параметр, принимающий три значения р, q, г, и имеет два состояния а и b; матрицы переходных вероятностей таковы:

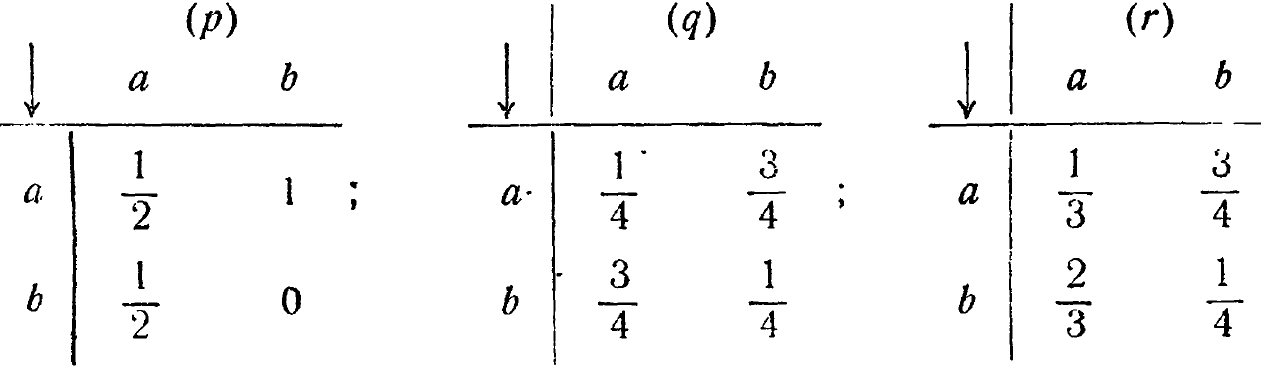
Машина начинает движение в состоянии b, делает один шаг со входом р, затем один шаг со входом q и затем один шаг со входом р. Каковы вероятности того, что она придет в а или в b?

*Упр. 4. (Продолжение.) Какое общее правило, использующее умножение матриц, позволяет получить ответ алгебраически? (Указание: упр. 9/6/8.)

Упр. 5. Соедините марковскую машину (с состояниями a, b, с и входными состояниями )

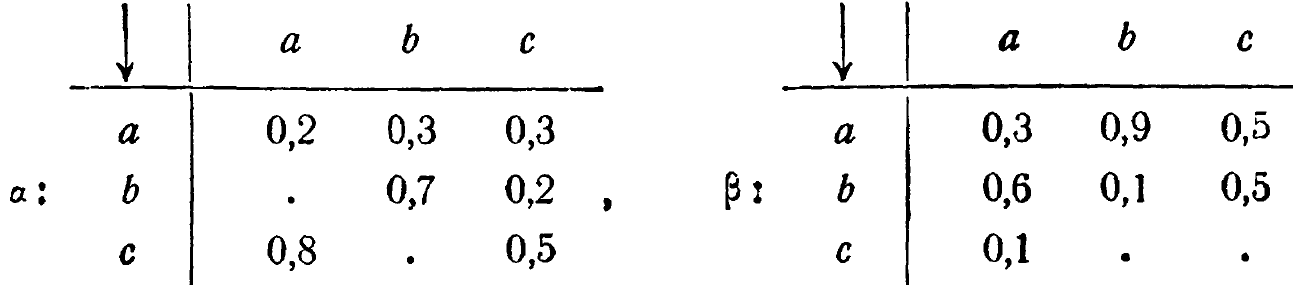
с марковской машиной (с состояниями е,f и входными состояниями )

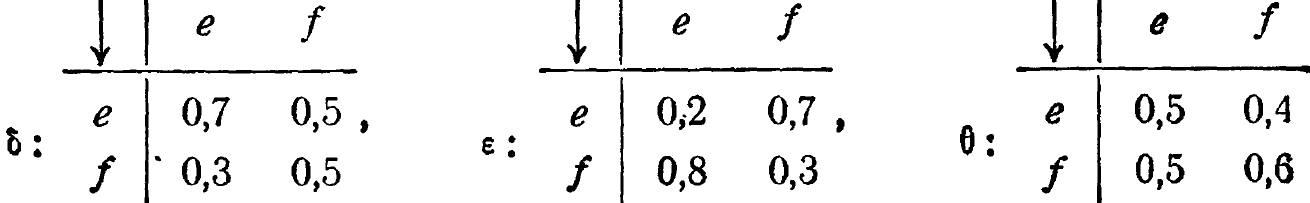
посредством  преобразования   

Какая марковская машина (без входа) получится? (Указание: попробуйте изменить вероятности на 0 и 1, чтобы истема стала детерминированной, и примените метод 4/8; затем сделайте вероятности дробными и используйте тот же основной метод.)

Упр. 6. (Продолжение.) Должна ли новая матрица оставаться марковской?

*Упр. 7. Если М - марковская машина, доминирующая над детерминированной машиной N, то покажите, что выходы N становятся цепью Маркова лишь после того, как М приходит к статистическому равновесию (в смысле 9/6).