4/7. Проследим теперь операцию соединения подробно. Предположим, что машину (преобразователь) Р требуется соединить с другой машиной R. Пусть для простоты машины Р должна действовать на R, не .вызывая обратного действия R на Р; примером может послужить соединение микрофона с усилителем или прорастание двигательного нерва для иннервации эмбриональной мышцы. Мы должны соединить выход из Р со входом в R. Очевидно, что поведение R, или, точнее, преобразование, описывающее изменение состояний R, будет за-висеть от состояния Р и изменяться вместе с ним. Отсюда следует, что машина R должна иметь параметры в качестве входа и что значения этих параметров в каждый момент должны быть некоторой функцией состояния Р. Положим для определенности, что машина,или преобразователь, R имеет три преобразования, перечисленные в 4/1, т. е.

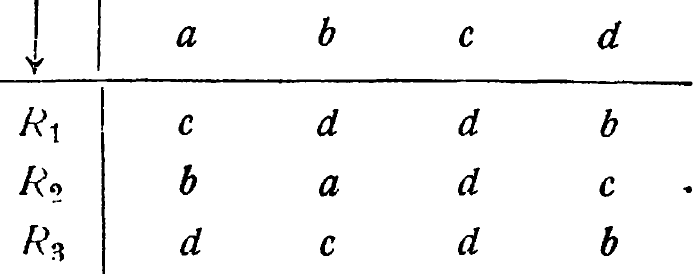
Положим также, что Р имеет преобразование для трех
состояний i, j, k:

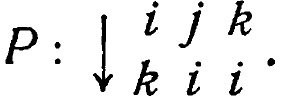
Мы должны теперь соединить машины Р и R, указав,какое значение должен принимать параметр машины R (назовем его а), когда Р находится в любом из своих состояний. Положим, что мы связали их соотношением Z (однозначным, но не замкнутым преобразованием) :

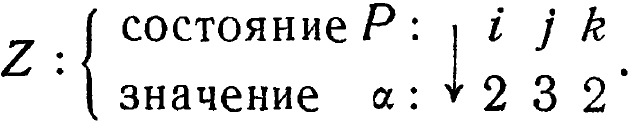
(Соотношение между Р и а сделано несколько нерегулярным, чтобы подчеркнуть, что детали здесь совершенно произвольны и полностью определяются тем, кто производит соединение.) Положим далее (это существенно для упорядоченности соединения), что две наши машины Р и R работают по общей временной шкале, так что изменения в них идут шаг в шаг.

Теперь нетрудно видеть, что две наши машины образуют одну новую машину с вполне детерминированным поведением. Так, предположим, что вся система начинает работу, когда R находится в состоянии а, а Р - в состоянии i. Поскольку Р находится в состоянии Z, то в машине R будет осуществляться преобразование R2 (согласно соотношению Z). Это изменит а в b; в то же время i в Р перейдет в k, так что состояния а и i детерминированно перейдут в b и k. Теперь повторяем рассуждение. Поскольку Р находится в состоянии k, то в машине R опять (согласно соотношению Z) будет осуществляться преобразование R2; поэтому b перейдет (при R2) в a, a k перейдет (при Р) в i. Это приведет всю систему в целом в начальное состояние (а, i), после чего система, очевидно, будет двигаться неограниченно долго по этому циклу.

Поведение всей машины станет более очевидным, если мы применим метод 3/5 и увидим, что состояние целой машины есть просто вектор с двумя составляющими (х,у), где х - одно из состояний a, b, с, d, а у - одно из состояний i, j, k. Таким образом, вся машина имеет двенадцать состояний, а выше было показано, что состояние (a,i) испытывает переходы (a,i) (b, k) (a,i) и т. д.

Упр. 1. Пусть Q - преобразование нашей целой машины с двенадцатью состояниями (х, у); выпишите Q полностью.

Упр. 2. (Продолжение.) Начертите кинематический график Q. Сколько в нем бассейнов?

Упр. 3. Соедините Р и R, используя преобразование У:

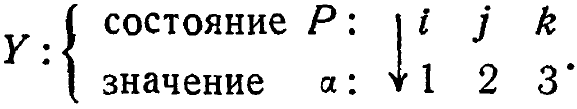
Что случится, если машина начнет работу с состояния (а, i)?

Упр. 4. Если две машины соединены в одну систему, то зависит ли поведение всей системы от способа соединения? (Указание: используйте предыдущее упражнение.)

Упр. 5. Если две машины с числом состояний соединены вместе, то какова максимальная длина переходного процесса, который может возникнуть во всей системе?

Упр. 6. Если максимальная длина переходного процесса в машине М равна n состояниям, то какова максимальная длина переходного процесса в машине, образованной соединением трех машин М вместе?
Упр. 7. Возьмите много частей (A, В, С,...), каждую с преобразованием

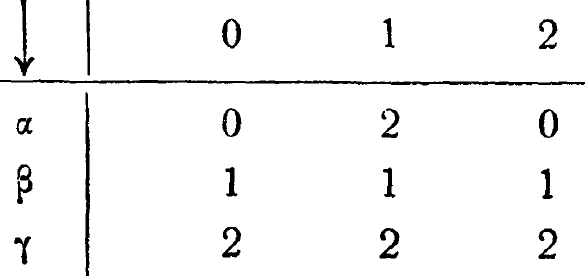
и соедините их в одну длинную цепь.

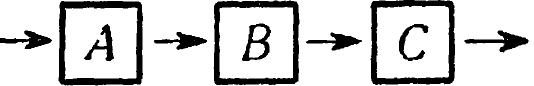вход и т.д.

Пусть в этой цепи часть А действует на В, В - на С и т. д. согласно

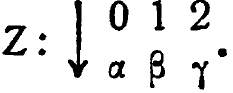
Если вход в А имеет значение , что случится с состояниями дальше по цепи?

Упр. 8. (Продолжение.) Что случится, если вход изменит через один шаг свое значение с на , а затем вернется опять в , где и останется?