ГЛАВА 3. Векторы

3/10. Фазовое пространство. Если составляющими вектора служат числовые переменные, то преобразование можно представить в геометрической форме; и иногда эта форма обнаруживает некоторые свойства гораздо более ясно и очевидно, чем рассмотренные до сих пор алгебраические формы.

В качестве примера рассмотрим преобразование

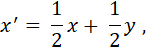
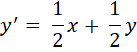
из упр. 3/6/7. Выбрав оси х и у, мы можем представить любой данный вектор, например (8,4), точкой, у которой абсцисса равна 8, а ордината 4. Таким образом, начальное состояние системы может быть представлено точкой Р на рис. 3/10/1 (I).

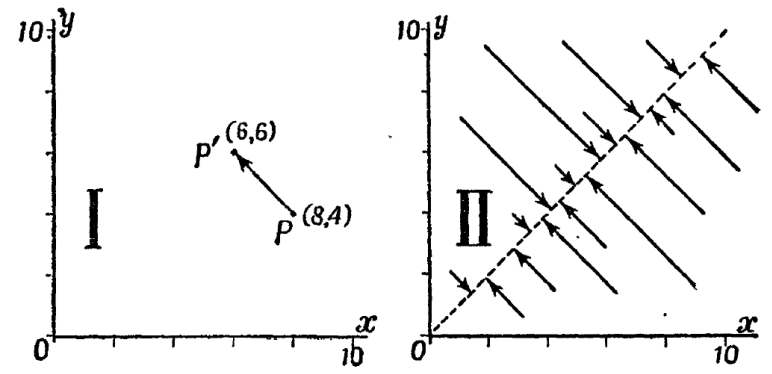
Рис. 3/10/1

Преобразование превращает этот вектор в (6,6) и тем самым превращает состояние системы в состояние, отвечающее точке Р'. Конечно, это движение есть не что иное, как изменение, изображенное на кинематическом графике в 2/17; только теперь оно изображено на плоскости с прямоугольными осями и числовым масштабом. Это двумерное пространство, в котором операнды и образы можно изобразить точками, называется фазовым пространством системы. (Свобода <пуговиц и ниток>, о которой говорилось в 2/17, здесь уже невозможна.)

На том же рисунке под цифрой II показано достаточно стрелок, чтобы определить в общем виде, что происходит, когда преобразуется любая точка. Здесь стрелки показывают другие изменения, которые произошли бы при выборе других состояний в качестве операндов. Легко увидеть и легко доказать геометрически, что все стрелки в этом случае задаются одним правилом: какая бы точка ни была выбрана в качестве опе-ранда, проводите из нее стрелку под углом в 45° влево вверх (или вправо вниз) до пересечения с диагональю, представленной линией у = х.

Теперь ясна польза фазового пространства (II): оно позволяет с первого же взгляда обозреть все траектории системы, как бы застывшие в единой картине. Благодаря этому часто бывает очень легко обнаружить какое-нибудь свойство или доказать какой-нибудь тезис там, где алгебраическая форма была бы неясной.

Представление на плоскости возможно только в том случае, когда вектор имеет две составляющие. При трех составляющих часто может оказаться полезным представление на трехмерной модели или на перспективном чертеже. Когда число составляющих больше трех, действительное представление уже невозможно, но принцип сохраняется, и схема, изображающая такую многомерную структуру, все еще может быть в высшей степени полезной, особенно когда нас интересуют не столько частные, сколько общие, топологические свойства.

[Словами <фазовое пространство> иногда обозначается пустое пространство, в которое еще не внесены стрелки (т. е. пространство, в которое может быть внесено любое множество стрелок); иногда этими словами обозначается диаграмма, содержащая множество стрелок, свойственное Данному преобразованию, подобно приведенной выше диаграмме II. Обычно из контекста ясно, какое значение имеется в виду.]

Упр. Набросайте схемы фазовых пространств, достаточно подробные. чтобы показать основные черты некоторых систем из 3/4 и 6.