ГЛАВА 3. Векторы

3/11. Что такое <система>? В 3/1 было сказано, что каждая реальная детерминированная машина или динамическая система соответствует замкнутому однозначному преобразованию; последующие параграфы иллюстрировали это положение многочисленными примерами. (Отсюда, однако, не следует, что такое соответствие всегда очевидно; напротив, любая попытка применить это положение в общем виде столкнется очень скоро с определенными трудностями, которые мы сейчас рассмотрим.

Предположим, что мы имеем перед собой определенную реальную динамическую систему - качающийся маятник, или растущую культуру бактерий, или автопилот, или туземную деревню, или сердечно-легочный препарат. Предположим, что мы хотим найти соответствующее преобразование, начиная с самого начала и исходя лишь из основных принципов. Пусть, например, наша система - простой маятник длиной в 40 см. Выбрав подходящее записывающее устройство, мы отводим маятник на 30° в сторону, отпускаем его и каждые четверть секунды записываем его положение. Мы находим последовательные отклонения: 30°, 10° и -24° (по другую сторону). Поэтому первой нашей оценкой преобразования при данных условиях будет

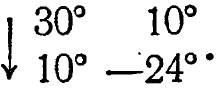
Затем, как хорошие ученые, мы исследуем переход от 10°: отводим маятник в сторону на 10°, отпускаем и обнаруживаем, что через четверть секунды отклонение равно +3°! Очевидно, что изменение от 10° неоднозначно - система сама себе противоречит. Что же нам теперь делать?
Наше затруднение типично для научных исследований и носит принципиальный характер: мы хотим, чтобы преобразование было однозначным, но это не получается.

Мы не можем отказаться от требования однозначности, ибо это значило бы отказаться от надежды делать однозначные предсказания. К счастью, опыт давно уже показал, что надо делать: надо переопределить систему.

Здесь мы должны ясно представить себе, как должна определяться <система>. Первое наше побуждение - показать на маятник и сказать: <Система есть вот эта вещь>. Этот метод имеет, однако, принципиальный недостаток: каждый материальный объект содержит не менее чем бесконечное число переменных и, следовательно, не менее чем бесконечное число возможных систем. Например, реальный маятник имеет не только длину и положение - он имеет также массу, температуру, электропроводность, кристаллическую структуру, химические примеси, некоторую радиоактивность, скорость, отражательную способность, прочность на разрыв, пленку влаги на поверхности, зараженность бактериями, оптическое поглощение, упругость, контур, удельный вес и т. д. Требование изучить <все> эти факты не осуществимо, и в действительности никто никогда не предпринимал таких попыток. Нам необходимо выбрать и изучить лишь факты, представляющие для нас интерес с точки зрения определенной, заранее указанной цели.

Истина состоит в том, что в окружающем нас мире лишь некоторые множества фактов могут давать замкнутые однозначные преобразования. Обнаружить такие множества иногда легко, иногда трудно. История науки и даже история любого отдельного исследования изобилуют примерами этого. Обычно обнаружение таких множеств связано с другим методом определения системы - с методом перечисления переменных, которые должны приниматься в расчет. Система теперь означает не вещь, а перечень переменных. Этот перечень может изменяться, и обычнейшая задача экспериментатора состоит в том, чтобы изменять перечень (<принимать в расчет другие переменные>), пока не будет найдено множество переменных, обеспечивающее требуемую однозначность. Так, мы сначала рассматривали маятник, как если бы он состоял только из одной переменной <угловое отклонение от вертикали>; мы обнаружили, что определенная таким образом система не обладает однозначностью. Если бы мы хотели продолжать, мы попробовали бы ввести другие определения, например вектор:
(угловое отклонение, масса маятника), который также оказался бы неподходящим. В конце концов мы попробовали бы вектор:
(угловое отклонение, угловая скорость) и нашли бы, что определенные по такому способу состояния дадут нам желаемую однозначность (см. упр. 3/6/14).

Некоторые из таких открытий отсутствующих переменных имели величайшее научное значение, например когда Ньютон открыл значение количества движения или когда Гоулэнд Гопкинс (1) открыл значение витаминов (поведение крыс при диете не было однозначным, пока витамины не были опознаны). Иногда такое открытие в научном отношении тривиально, например когда однозначные результаты получаются после того, как из водоснабжения устраняется примесь или завинчивается недостающий винт; но однозначность всегда существенна.

[Иногда требуется лишь однозначность некоторых вероятностей. Это более тонкое требование затрагивается в 7/4 и 9/2. Но оно не противоречит сказанному выше; оно просто означает, что интересующей нас переменной является сама вероятность, а не переменная, за-дающая вероятность. Так, если я научно изучаю рулетку, меня может интересовать переменная <вероятность того, что в следующий раз выпадет красное>, которая имеет числовые значения в интервале от 0 до 1, а не переменная <цвет, который выпадет в следующий раз>, которая имеет только два значения: <красное> , и <черное>. Система, включающая последнюю переменную, почти наверное непредсказуема, тогда как система, включающая первую переменную (вероятность), может быть вполне предсказуемой, ибо указанная вероятность имеет постоянное значение, приблизительно равное 1/2.]

<Абсолютная> система, описанная и использованная в книге <Устройство мозга>, является именно таким множеством переменных.

Теперь ясно, почему мы можем сказать, что каждая детерминированная динамическая система соответствует однозначному преобразованию (хотя мы отнюдь не осмеливаемся выставлять какие-либо догмы о том, что содержит в себе реальный мир, ибо он полон неожиданностей). Мы можем сказать это просто потому, что наука отказывается изучать другие типы, вроде упомянутого маятника с одной переменной, отвергая их как <хаотические> и <бессмысленные>. Мы и только мы окончательно решаем, что нам признавать за <похожее на машину> и что не признавать (этот вопрос резюмируется в 6/3).

1 Фредерик Гоулэнд Гопкинс (1861-1947) - английский биохимик; одним из первых исследовал витамины (в 1906-1912 гг.).- Прим, перёв. Зак. 3346. У. Росс Эшби