3/9. <Неразрешимые> уравнения>. Упражнения 3/6 с несомненностью показывают, что если дано замкнутое однозначное преобразование, а также некоторое начальное состояние, то траектория, начинающаяся из этого состояния, является вполне определенной (т. е. однозначной) и может быть вычислена. В самом деле, пусть х - начальное состояние, а Т-преобразование; тогда последовательные значения (траектория) х образуют ряд
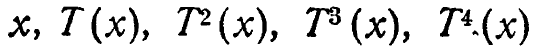и т. д.

Этот процесс определения траектории по заданному преобразованию и заданному начальному состоянию называется <интегрированием> преобразования. (Этот термин особенно употребляется в том случае, когда преобразование есть множество дифференциальных уравнений, как в 3/7; весь процесс называется тогда также <решением> уравнений.)

Если читатель проработал весь 3/6, то, вероятно, он уже убедился в том, что, имея преобразование и начальное состояние, можно всегда получить траекторию, Поэтому он не будет обескуражен, услышав, что некоторые уравнения называются <неинтегрируемыми> или <неразрешимыми>. Эти слова имеют чисто технический смысл и означают только, что траектория не может быть определена, если мы ограничены некоторыми определенными математическими операциями. В своем труде <Механизм экономических систем> Тастин (1) ясно показывает, как экономист может стремиться изучить системы и уравнения, принадлежащие к типу <неразрешимых>; и он показывает, как экономист может на практике добиться желаемого.

1 Арнольд Тастин (род. 1899) - английский ученый, специалист в области автоматики и электронной техники. - Прим, перев.