3/7. (Этот параграф может быть опущен.) Предыдущий параграф имеет фундаментальное значение, ибо он является введением в методы математической физики, в том виде, как они применяются к динамическим системам. Поэтому мы настоятельно советуем читателю проработать все упражнения: только таким путем можно действительно усвоить излагаемые принципы. Проделав это, он будет лучше подготовлен к усвоению настоящего параграфа, в котором подытоживается описываемый метод.

Физик начинает с наименования своих переменных: . После этого основные уравнения преобразования всегда могут быть получены следующим основным методом:

1)     Взять первую переменную и рассмотреть, каково будет ее следующее состояние. Если она изменяется конечными шагами, то ее следующее состояние будет , а если она изменяется непрерывно, то следующее состояние будет + d (вместо этого в последнем случае мы можем рассмотреть значение d/dt).

2)     Используя все, что известно о данной системе, а также законы физики, выразить значение или d/dt (т. е. нового состояния переменной ) через значения, которые (и любые другие необходимые факторы) имеют сейчас. Таким путем получаются такие уравнения, как
=2а - или d/dt = 4ksin.

3)     Повторять этот процесс поочередно для каждой переменной, пока не будет выписано все преобразование.

Полученное таким образом множество уравнений (задающее для каждой переменной в системе следующее состояние этой переменной, выраженное в виде функции значений переменных и от любых других необходимых факторов) есть каноническое представление системы. Это - стандартная форма, к которой могут быть приведены все описания детерминированной динамической системы.

Если все функции в каноническом представлении линейны, то система называется линейной.

При заданном начальном состоянии траектория, или линия поведения, может быть вычислена нахождением степеней преобразования, как в 3/9.

*Упр. 1. Переведите данное преобразование из канонической формы

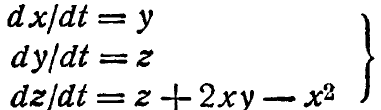
в дифференциальное уравнение третьего порядка с одной переменной x. (Указание: исключите у и z и их производные.)

*Упр. 2. Уравнение простого гармонического колебания часто записывается в виде -

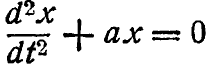
Переведите его в каноническую форму с двумя независимыми переменными. (Указание: обратите процесс, использованный в упр. 1.)

*Упр. 3. Переведите уравнение

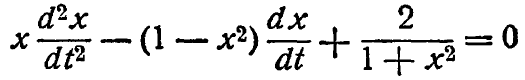
в каноническую форму с двумя переменными.