11/5. Можно ли вывести некоторый общий принцип для способов игры упомянутого R и его видов на успех?

Если в таблице допускается полная свобода расположений, то возможности станут столь многочисленны, произвольны и сложны, что вряд ли можно высказать о них что-либо общее. Однако имеется определенный тип таблиц, допускающий точную формулировку и вместе с тем достаточно общий, чтобы представлять интерес.
(В то же время он является основным в теории регулирования.)

Исключим из всех возможных таблиц те, которые делают игру нашего R слишком легкой и поэтому неинтересной. Упр. 11/4/3 показывает, что если столбец в таблице содержит одинаковые исходы, то игра нашего R не обязательно должна быть <различающей>, т. е. R не обязательно должен менять свой ход с каждым изменением хода игрока D. Будем, следовательно, рассматривать только такие таблицы, где ни один столбец не содержит двух одинаковых исходов. В этом .случае R должен выбирать ход, полностью зная ход упомянутого D, т. е. любое изменение хода D необходимо требует изменения хода нашего R. (При этом не делается никаких допущений о соотношениях между исходами одного столбца и исходами другого столбца, так что на эти соотношения не накладывается никаких ограничений.) Такова, например, таблица 11/5/1. Пусть теперь задана некоторая цель и R выбирает, каким будет его ход в ответ на каждый ход игрока D.
Таблица 11/5/1

Очень важно, что, выигрывая или проигрывая, он должен выбрать один и только один ход в ответ на любой возможный ход игрока D. Его выбор ходов, или <стратегия>, как это можно назвать, может выглядеть следующим образом:

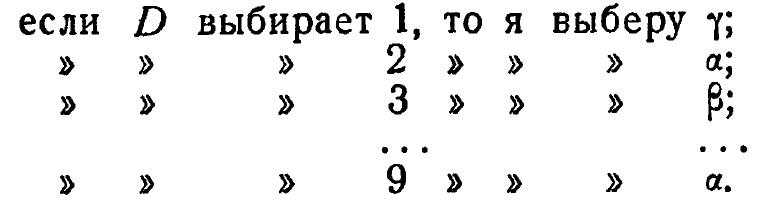
Тем самым он, конечно, определяет некоторое преобразование .(которое должно быть однозначным, ибо R не может делать одновременно два хода):

Это преобразование определяет единственным образом некоторое множество исходов. В это множество войдут исходы, которые бы встретились фактически, если бы D в некоторой последовательности игр делал каждый возможный шаг по крайней мере один раз. Ибо 1 и у дают исход k, и 2 и ? дают опять k и т. д., что приводит к преобразованию

Теперь можно высказать утверждение, что разнообразие этого множества исходов не может быть меньше, чем частное
разнообразие ходов игрока D
разнообразие ходов игрока R
т. е. в данном случае разнообразие множества исходов не может быть меньше .

Это утверждение легко доказать. Предположим, что R отмечает один элемент в каждой строке и стремится просто к тому, чтобы удерживать разнообразие отмеченных элементов сколь возможно малым (оставляя пока в стороне всякое понятие о цели). Он отмечает некоторый элемент в первой строке. Во второй строке он должен перейти к новому столбцу, если он не хочет увеличить разнообразие отмеченных элементов добавлением к ним нового, отличного от них элемента. Ведь в первоначально выбранном столбце все элементы по предположению различны. Чтобы сохранять разнообразие в один элемент, R должен в каждой строке переходить к новому столбцу. (Это лучшее, что он может сделать. Иногда такого перехода от столбца к столбцу будет недостаточно, чтобы сохранить разнообразие в один элемент; но для нашего рассуждения это неважно: поскольку нас интересует лишь наименьшее возможное разнообразие, мы допускаем, что обстоятельства складываются как можно благоприятнее.) Если R имеет n возможных ходов (в нашем примере три) и на n-й строке все столбцы использованы, то для следующей строки один из столбцов нужно использовать снова, так что придется ввести но-вый исход в наше множество отмеченных исходов. Например, в таблице 11/5/1 выбор элемента k в первых трех строках позволит сохранять разнообразие в один элемент, но на четвертой строке придется ввести второй элемент в наше множество исходов.

Обобщаем. Если:
а) никакие два элемента в одном и том же столбце не являются одинаковыми,
б) R выбирает множество исходов, по одному из каждой строки,