11/3. Игра и исход. Забудем поэтому все, что мы знаем о регулировании, и предположим просто, что мы наблюдаем за двумя игроками R и D, участвующими в какой-то игре. Мы будем следить за успехами игрока R, который пытается выиграть некое а. Правила игры следующие. У игроков имеется таблица 11/3/1:
Таблица 11/3/1

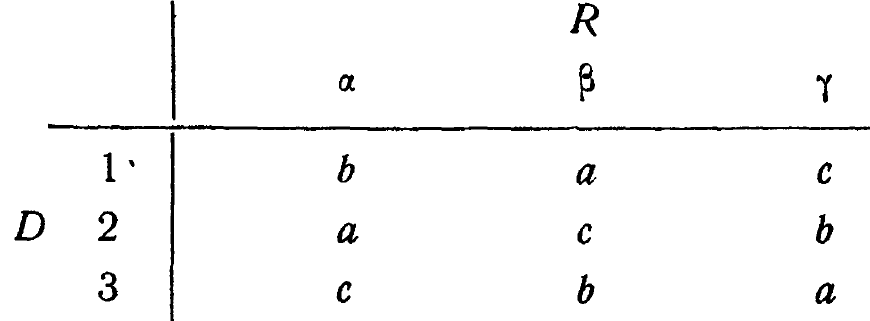
которую могут видеть оба игрока. D начинает, выбирая цифру и тем самым некоторую строку таблицы. R, зная эту цифру, выбирает затем греческую букву и тем самым некоторый столбец. Курсивная латинская буква, стоящая на пересечении строки и столбца, является исходом. Если исходом будет а, то R выигрывает; если нет, то R проигрывает.

Рассмотрение таблицы быстро показывает, что при данной таблице игрок R всегда может выиграть. Какое бы значение игрок D ни выбрал сначала, игрок R всегда может выбрать такую греческую букву, которая даст ему желаемый исход.

Так, если D выбирает 1, то R выбирает р; если D выбирает 2, то R выбирает а и т. д. В самом деле, если R действует в соответствии с преобразованием

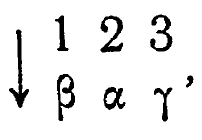
то он всегда может получить исход а.
При такой таблице положение нашего R исключительно выгодно, ибо R не только может всегда получать исход а, но -он может так же легко получать, если нужно, исходы b или с; R фактически полностью контролирует исход игры.

Упр. ,1. Какое преобразование должен использовать R, чтобы получать всегда исход с?

Упр. 2. Пусть R и D - переменные, значениями которых служат целые числа, и пусть исход Е также есть целое число, задаваемое соотношением
E=R-2D:
Выразите R через D, если желаемый исход равен 37.

Упр. 3. Задние колеса какого-то автомобиля скользят. Пусть D - переменная, называемая <стороной, в которую движется задняя часть автомобиля>, и принимающая два значениям <направо> и <налево>. Пусть R - действие водителя, называемое <выбором направления, в котором он поворачивает рулевое колесо>, и принимающее два значения: <направо> и <налево>. Постройте таблицу размером 2 X 2 и проставьте исходы.

Упр. 4. Если игра R определяется игрой D в соответствии с преобразованием

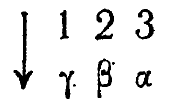
и сыграно много партий, то каково будет разнообразие встречающихся исходов?

Упр. 5. Полностью ли R контролирует исходы, если таблица <триединая>? (см. упр. 4/2/4).