9/14. Некоторая путаница возникает иногда из-за того, что шеннонова мера <энтропии>, взятая для множества вероятностей p1, р2,..., есть сумма членов pi log pi умноженная на -1, тогда как <количество информации>, определенное Винером в его <Кибернетике>, есть та же самая сумма членов pilog pi, но без перемены знака (т. е. умноженная на +1). (Следует иметь в виду, что р log р всегда отрицательно, так что множитель <-1> превращает его в положительное число.)

Однако здесь не должно быть никакой путаницы, ибо основные идеи одинаковы. Оба автора рассматривают информацию как <то, что устраняет неопределенность>> и оба измеряют ее количеством неопределенности, которую она устраняет. Далее, оба занимаются в основном приростом или увеличением информации, имеющим место при получении сообщения, в то время как абсолютные количества, наличествующие до или после этого, представляют меньший интерес.

Ясно, что когда вероятности распределены разбросанно, как в диаграмме А на рис. 9/14/1, неопределенность больше, чем когда они распределены компактно, как в диаграмме В. Получение сообщения, заставляющего получателя изменить от распределения А к распределению В свою оценку того, что должно произойти, содержит положительное количество информации.

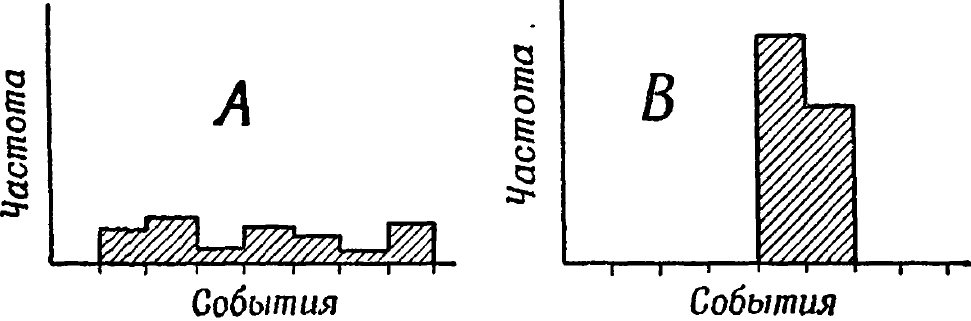
Рис. 9/14/1.

Но выражение 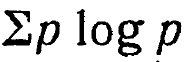(где знак  означает сумму), примененное к А, дает более отрицательное число, чем в применении к В; оба значения суммы будут отрицательными, но первое будет больше по абсолютной величине. Так, распределение А может дать сумму, равную -20, а распределение В - сумму, равную -3. Согласимся в качестве количества информации, связанного с каждым распределением, т. е. с каждым множеством вероятностей, взять 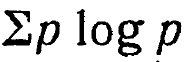, умноженное на +1. Так как, вообще говоря,

прирост (чего угодно) = окончательному количеству минус начальное количество,

то прирост информации в этом случае будет равен (-3) -(-20), т. е. +17.

Следовательно, мы получим положительное число, как и хотели. Таким образом, рассматриваемая с этой винеровской точки зрения величина 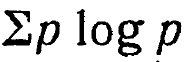должна умножаться на +1, т. е. оставаться неизмененной; тогда мы вычислим прирост.

Шеннон же в своей книге занимается особым случаем, в котором получаемое сообщение известно с определенностью. В этом случае все вероятности равны нулю, за исключением единственной, равной 1. Для такого множества сумма  log р равна нулю, так что окончательное количество равно нулю и прирост информации равен

0 - (начальное количество).

Другими словами, информация в сообщении, которая равна приросту информации, есть сумма 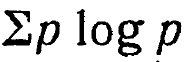, вычисленная для начального распределения и умноженная на - 1, что и дает шеннонову меру.

Таким образом, между двумя этими мерами существует не больше несоответствия, чем между двумя способами измерения того, <насколько точка Q расположена правее точки Р> (см. рис. 9/14/2). Можно считать,

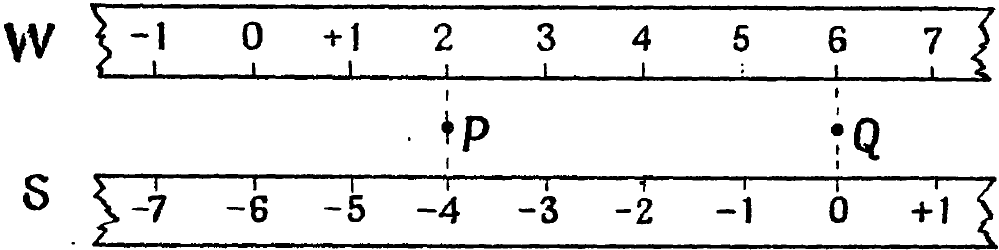
Рис. 9/14/2.
что Р и Q здесь соответствуют двум степеням неопределенности, причем большей определенности отвечает точка справа, а сообщение перемещает получателя из

Р в Q.

Расстояние между Р и Q может быть измерено двумя способами, которые, очевидно, эквивалентны. По способу Винера линейка прикладывается к Р и Q (как линейка W на рисунке), и тогда расстояние, на которое Q лежит правее Р, равно разности (отсчет для Q) минус (отсчет для Р).

По способу Шеннона (линейка S на рисунке) нуль прикладывается к Q, и тогда расстояние, на которое Q лежит правее Р, таково: минус (отсчет для Р).
Ясно, что между этими двумя способами нет на самом деле никакого несоответствия.