
9/8. Перекодирование в марковскую форму. Если оказывается, что в траекториях системы переходные вероятности зависят некоторым постоянным образом от состояний,, непосредственно предшествующих каждому операнду, то эту немарковскую систему можно сделать марковской, применяя метод, более существенный, чем может показаться на первый взгляд, а именно - переопределяя систему.
Пусть, например, в системе типа упр. 9/7/1 переходы таковы, что по окончании последовательности двух состояний ...СС система всегда переходит в D, независимо от того, что было раньше; после же ...DC она всегда переходит в С, а после ...CD она с одинаковой частотой (если взять достаточно длинный отрезок) переходит в С или D и то же самое после ...DD. Нам здесь нужно лишь определить новые состояния как векторы с двумя составляющими: предшествующим состоянием в качестве первой составляющей и последующим состоянием в качестве второй составляющей. Так, если первоначальная система прошла траекторию, оканчивающуюся на ...DC, мы скажем, что новая система находится в состоянии (Z), С). Если первоначальная система перейдет затем в состояние С, так что траектория ее будет иметь вид ...DCC, то мы скажем, что новая система перешла в состояние (С, С). В целом же новая система совершила переход (D, С) ![]() (С, С). Эти новые состояния уже будут образовывать цепь Маркова, ибо их вероятности (как мы допустили) не зависят от предшествующих состояний; и в самом деле матрица их будет иметь вид
(С, С). Эти новые состояния уже будут образовывать цепь Маркова, ибо их вероятности (как мы допустили) не зависят от предшествующих состояний; и в самом деле матрица их будет иметь вид
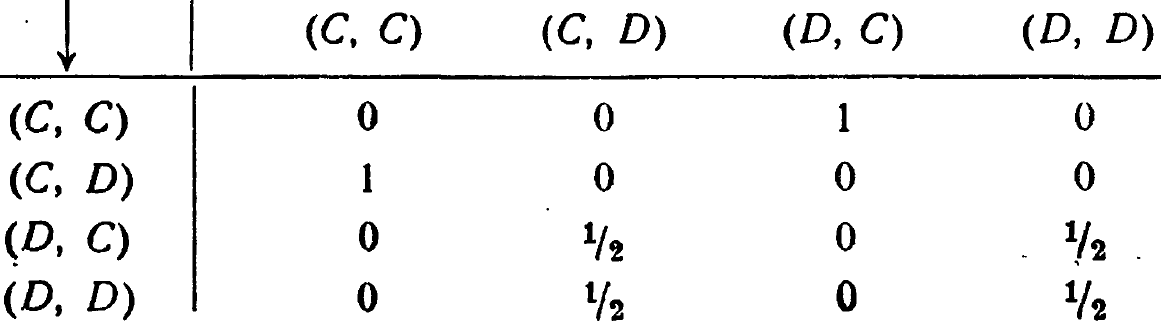
[Заметим, что переход (С, D)![]() (С, D) невозможен, ибо любое состояние, оканчивающееся на (-,D), может перейти только в состояние, начинающееся с (D,-). Некоторые другие переходы также невозможны в новой системе.]
(С, D) невозможен, ибо любое состояние, оканчивающееся на (-,D), может перейти только в состояние, начинающееся с (D,-). Некоторые другие переходы также невозможны в новой системе.]
Если в другой системе вероятности перехода зависят от состояний, встречавшихся на n предыдущих шагах, то новые состояния должны определяться как векторы из n последовательных состояний.
Этот метод переопределения системы может показаться искусственным и бесцельным. В действительности же он имеет первостепенное значение, поскольку он переводит наше внимание от системы с недетерминированными состояниями к системе с детерминированными состояниями. Поведение новой системы более предсказуемо, ибо ее <состояния> учитывают прошлую историю первоначальной системы. Так, в первоначальной форме, зная, что система находится в состоянии С, можно было сказать только, что она может перейти либо в С, либо в D. Во второй форме знание того, что система находится в состоянии (D, С), позволяет предсказать ее поведение с такой же определенностью, с какой можно было бы предсказать поведение системы в первоначальной форме, зная, какие состояния имели место раньше. Здесь важно отметить следующее обстоятельство. Наш метод переопределения показывает, что два способа <знать> систему - по ее нынешнему состоянию или по ее прошлой истории - связаны друг с другом вполне определенной, точной зависимостью. В теории неполностью наблюдаемой системы (6/21) это обстоятельство использовалось по существу таким же образом. Итак, мы опять приходим к заключению, что наличие <памяти> в реальной системе не является внутренним свойством системы; мы предполагаем ее наличие, когда наши возможности наблюдения ограничены. Сказать: <Мне кажется, что эта система имеет память>, - все равно что сказать: <Мои возможности наблюдения не позволяют мне делать достоверных предсказаний на основе одного наблюдения, но я могу делать достоверные предсказания после некоторой последовательности наблюдений>.
