ЭНТРОПИЯ 9/11. В 7/5 и в гл. 8 мы видели, что информация не может передаваться в большем количестве, чем это позволяет количество разнообразия.

Мы видели, что ограничения могут уменьшить потенциальное количество разнообразия. И мы только что видели в предшествующем параграфе, что такой источник разнообразия, как цепь Маркова, имеет нулевое ограничение разнообразия, когда все его переходы равновероятны. Отсюда следует,
что это условие (нулевого ограничения разнообразия) дает возможность источнику информации, если он ведет себя как цепь Маркова, передавать максимальное количество информации (в данное время).

Шеннон ввел меру количества разнообразия, обнаруживаемого на каждом шаге цепью Маркова. Эта мера, называемая энтропией, представляет, как выяснилось, огромную важность для многих вопросов, связанных с непрекращающейся передачей. Эта мера вводится следующим образом.

Если множество имеет некоторое разнообразие и мы выбираем из этого множества один элемент посредством некоторого определенного процесса выбора, то различные возможные результаты этого выбора будут связаны с различными соответствующими вероятностями. Так, пусть огни светофора имеют разнообразие в четыре элемента, обнаруживая комбинации:
1)     красный;
2)     красный и желтый;
3)     зеленый;
4)     желтый.

Пусть они горят соответственно в течение 25, 5, 25 и 5 сек. Тогда автомобилист, появляющийся неожиданно через нерегулярные промежутки времени, будет заставать светофор в различных состояниях с частотой примерно в 42,8,42 и 8%, соответственно. Взятые как вероятности, эти частоты будут иметь значения 0,42; 0,08; 0,42 и 0,08. Таким образом, состояние <зеленый свет> имеет (если применяется именно этот способ выбора) вероятность 0,42, и аналогично - другие состояния.

Обратно, любое множество вероятностей, т. е. положительных дробей, в сумме составляющих 1, может рассматриваться как соответствующее некоторому множеству, члены которого обнаруживают разнообразие. От вероятностей р1, р2, ..., pn Шеннон переходит к вычислению величины

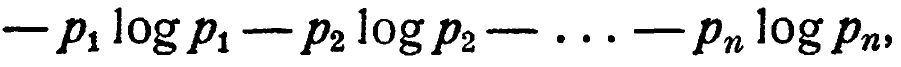
которую он называет энтропией множества вероятностей и обозначает символом Н.

Так, если взять десятичные логарифмы, то энтропия множества, связанного с огнями светофора, будет равна

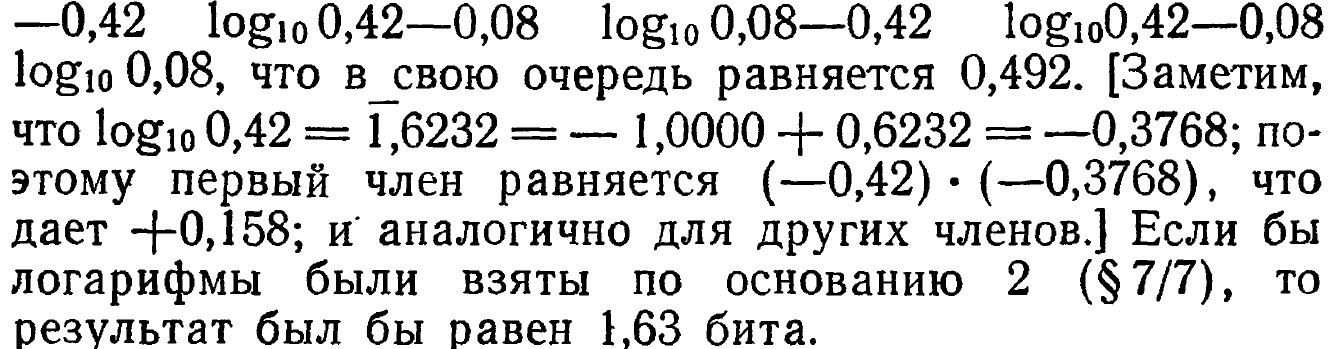
Слово <энтропия> будет применяться в этой книге, лишь в том смысле, в каком оно употреблялось Шенноном; любое более широкое понятие будет называться <разнообразием> или как-нибудь иначе.

Упр. 1. Из 80 случаев, когда я проезжал определенный железно-* дорожный переезд, он был закрыт в 14 случаях. Чему равна энтропия множества вероятностей?

Упр. 2. Из перетасованной колоды вытаскивается карта. Различаются три случая:
E1 - вытащен король треф;
E2- вытащена любая карта пик;
E3- вытащена любая другая карта.
Какова энтропия разнообразия различаемых случаев?

Упр. 3. Чему равна энтропия разнообразия одного бросания игральной кости?

Упр. 4. Чему равна энтропия разнообразия множества возможных исходов (с сохранением порядка) двух последовательных бросаний игральной кости?

Упр. 5. (Продолжение.) Чему равна энтропия n последовательных бросаний?

*Упр. 6. Чему равен предел - р log р, когда р стремится к нулю?