8/12. Передача за второй шаг. Итак, мы видели, что за один шаг разнообразие в U может увеличиться не больше чем на количество разнообразия в Т. Но что произойдет на втором шаге? Т может все еще иметь некоторое разнообразие; не перейдет ли и оно в Ut еще более увеличивая его разнообразие?

Возьмем простой пример. Предположим, что каждый элемент всего множества копий находится в одном из шести состояний , , 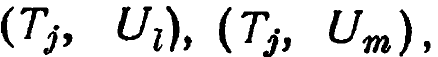так что все T находятся либо в  либо в Tj, либо в Tj, а все U находятся либо в Uk, либо в  , либо в Um. Система как целое - абсолютна. Поэтому все копии, находящиеся, скажем, в (Ti,Uk), будут при переходах от состояния к состоянию изменяться одинаково, принимая различные состояния совместно. То же самое относится и к копиям, находящимся в остальных пяти состояниях. Отсюда следует, что разнообразие состояний множества не может превышать 6, и это независимо от количества копий, входящих во множество; независимо от числа состояний в Т и U;, независимо от того, как долго могут продолжаться изменения. А отсюда следует, что разнообразие копий U никогда не может превышать шести U-состояний. Таким образом, коль скоро разнообразие в U возросло на количество разнообразия в Т, всякое дальнейшее возрастание должно прекратиться. Если все возрастание произошло за один шаг (как выше), то на втором шаге разнообразие больше не возрастает, хотя Т и может еще иметь некоторое разнообразие.

Следует отметить, какую важную роль в этом доказательстве играет спаривание состояний системы U с состояниями системы Т, т. е. выяснение того, какое значение Т и какое значение U встречаются в одной и той же машине. Очевидно, что простого знания количества разнообразия в Т и в U недостаточно для предсказания того, как они будут изменяться