13/9. Эти соображения применимы ко многим случаям регулирования.

Положим для определенности, что каждую минуту ванна может испытывать одно из трех отдельных возмущений:
a)     воздействие холодного воздуха,
b)     воздействие солнечных лучей,
c)     погружение холодного предмета.

Разнообразие равно трем, но это число вряд ли представляет разнообразие, которое фактически будет иметь место за длинный промежуток времени. За год, скажем, Большое Возмущение станет длинным вектором, быть может с несколькими сотнями составляющих. Например, одно из Больших Возмущений может быть вектором (т. е. последовательностью) с 400 составляющими (a, b, a, b, b, а, с, b, b, с, c,b,b, ..., c, b, а, b).

И если отдельные правильные ответы будут, соответственно , и , то Большой Ответ, соответствующий данному Большому Возмущению, будет вектором (т. е. последовательностью)

Если составляющие Большого Возмущения, взятые слева направо, не обнаруживают ограничения разнообразия, то все множество возможных Больших Возмущений имеет разнообразие ; и Большой Ответ должен иметь по крайней мере такое же разнообразие, чтобы регулирование было полным.

Мы теперь подошли к следующему обстоятельству; приведенная двойная последовательность, рассматриваемая в том порядке, в каком она появляется во времени, обнаруживает ограничение разнообразия, характерное для машины, т. е. она определяет машину с точностью до изоморфизма. Так, в только что приведенном примере события протекали в следующем порядке, слева направо:

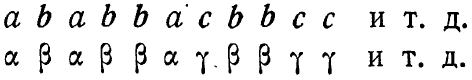
(Хотя и необязательно через равные промежутки времени.) Легко проверить, что эта последовательность, взятая как протокол, определяет машину со входом

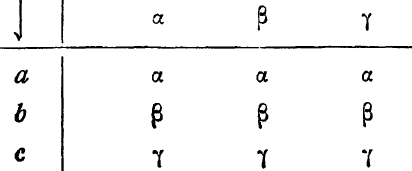
Таким образом, когда Большое Возмущение является вектором, все составляющие которого взяты из некоторого основного класса воздействий, то Большой Ответ есть либо вектор с таким же разнообразием, либо выход соответствующей машины со входом.