13/17. Выбор по этапам. Процесс выбора может быть более или менее растянут во времени. В частности, он может производиться дискретными этапами.

Водитель, выбирающий себе новый автомобиль, часто поступает именно так. Сначала он говорит, например: <Машина должна стоить менее 1000 фунтов> . Этот критерий вызывает некоторое ограничение числа возможностей. Затем он может добавить, что автомобиль должен вмещать пять человек и т. д. Каждый новый кри-терий уменьшает число оставшихся возможностей. Если он может купить только один автомобиль, то эти критерии в конце концов должны свести, все возможности к одной. Это сведёние необходимо осуществить любым способом, даже если для окончательного выбора придется прибегнуть к бросанию монеты.

Абстрактный выбор (или проектирование) машины также может протекать по этапам. Итак, предположим, что машина имеет четыре состояния: a, b, с, d. Преобразование

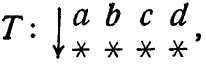
в котором звездочки еще не заменены конкретными состояниями, оставляет все возможности открытыми, Изменение его в преобразование

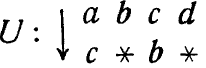
представляет собой частичный выбор. U также изображает множество преобразований, хотя и меньшее.Также будет обстоять дело и с преобразованием

 
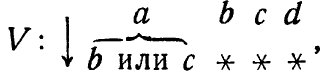
которое исключает все однозначные преобразования, содержащие переходы аа или ad. Таким образом, машина может быть выбрана по этапам, а этапы могут определяться различным образом. С количественной точки зрения здесь существенно, что общее количество осуществляемого при этом выбора не может превосходить сумму (измеряемых логарифмически) отдельных выборов. (Выбор измеряется сокращением разнообразия.) Так, если взять колоду карт и произвести сначала 2-битовый отбор, а затем 3-битовый, то для однозначного указания карты потребуется дальнейший отбор по крайней мере в 0,7 бита, ибо log2 52 = 5,7. Это ограничение абсолютно и (если речь идет о выборе машины) совершенно не зависит от типа машины или от способа выбора.

Упр. 1. Сколько возможностей устраняется, если к замкнутому однозначному преобразованию с состояниями а, b, с и с 27 первоначально возможными формами прибавить ограничение: <Оно не должно иметь состояний равновесия>?

Упр. 2. (Продолжение.) Если прибавить ограничение: <Оно должно иметь три состояния равновесия>?

Упр. 3. Сколько выбора, в логарифмической мере, было в упр. 1?

*Упр. 4. Чему равно количество выбора, если к абсолютной системе с n состояниями . где первоначально возможны все преобразования, добавляется ограничение: "Она не должна иметь состояний равновесия" <Она не должна иметь состояний равновесия>? (Указание: в какое число состояний, вместо первоначальных n состояний, может теперь перейти a1?) (ср. упр. 1).

Упр. 5. (Продолжение.) К чему стремится это количество, когда n стремится к бесконечности? (Указание: вычислите его для n = 10, 100, 1000.) (Эта оценка может применяться к машине 12/15.)

Упр. 6. Если, как описано в этом параграфе, карты в перетасованной колоде просматриваются (без дальнейшей тасовки) последовательно друг за другом в поисках одной определенной карты, то сколько информации приобретается в среднем при просмотре первой, второй, третьей и т. д. карты? (Систематический поиск.)

*Упр. 7. (Продолжение.) Сколько информации приобретается, если после каждого неудачного просмотра карта возвращается в колоду и колода тасуется перед просмотром следующей карты? (Случайный поиск.)