11/9. Небольшое видоизменение только что сформулированных теорем позволяет получить примечательное обобщение.

Рассмотрим тот случай, когда, даже если R ничего не делает (т. е. делает один и тот же ход при любом ходе своего противника D), разнообразие исходов меньше, чем разнообразие ходов D. Так именно обстоит дело при использовании таблицы 11/4/1. Если, скажем, R на все ходы партнера D дает ответ , то исходами будут a, b или d - разнообразие в три элемента, тогда как D имеет разнообразие в пять элементов. Чтобы получить возможность точного вычисления, предположим, что каждый элемент повторяется теперь в каждом столбце k раз (вместо <только одного> раза в 11/5). Точно такое же рассуждение, измененное лишь в том отношении, что теперь kn строк могут давать один и тот же исход, приводит нас к теореме о том, что
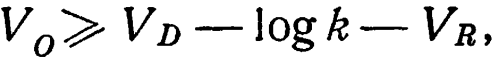где разнообразия измеряются логарифмически.
Совершенно аналогично можно модифицировать теорему об энтропиях, предполагая не как в 11/8, но

Тогда минимум Н(Е) будет равен H(D) - K - H(R) с аналогичной интерпретацией.