9/18. Приведем еще один пример, показывающий удивительную способность метода Шеннона проникать в самое существо проблем связи. Рассмотрим систему с состояниями а, b, с, d и с вероятностями переходов

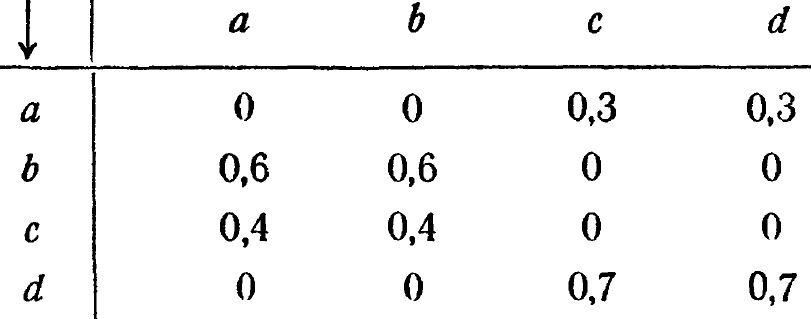
Типичной последовательностью будет

.. .bbbcabcabbcddacdabcacddddddabb... .

Равновесные вероятности будут соответственно равны 6/35, 9/35, 6/35, 14/35. Легко определить, что энтропия равна 0,92 бита на букву. Теперь предположим, что различие между а и d утрачивается; другими словами, кодируем нашу последовательность посредством преобразования

	a	b	c	d
	X	b	c	X

Вы скажете, что какая-то информация должна быть потеряна? Посмотрим! Отныне у нас имеется только три состояния: X, b, с, где X означает <либо а, либо d>. Так, приведенное выше сообщение будет теперь начинаться отрезком ...bbbcXbcXbbcXXXc.... Новые переходные вероятности будут равны

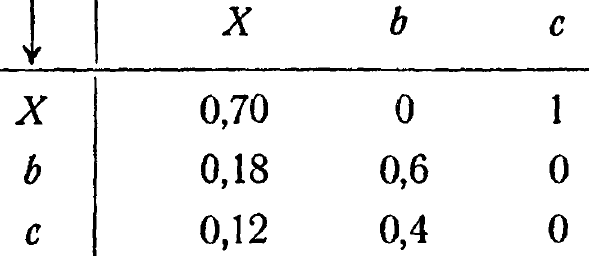
[сХ должно равняться 1, поскольку с всегда переходит либо в а, либо в d; переходы от а и от d должны быть взвешены (равновесными) вероятностями пребывания системы в данный момент в а или в d]. Новые состояния имеют следующие равновесные вероятности: состояние X - вероятность 20/35; состояние b - вероятность 9/35,; состояние с - вероятность 6/35; отсюда находим энтропии: Нх = 1,173; Нb= 0,971; Нс = 0. Итак, энтропия нового ряда будет равна 0,92 - такое же значение, как и раньше!

Это обстоятельство недвусмысленно показывает, что при слиянии состояний d и а в одно состояние X не теряется никакой информации. Это значит, следовательно, что должен существовать способ восстановления первоначального четырехбуквенного сообщения из трехбуквенного, т. е. способ определения, какие состояния X раньше были состояниями а, а какие - состояниями d. Более внимательное исследование показывает, что такое восстановление действительно может быть сделано и тем самым полностью подтверждает это достаточно удивительное предсказание.