7/25. Закон накопления опыта. В предыдущем параграфе было показано, что разнообразие в машине (когда дано некоторое множество) не может увеличиваться и обычно уменьшается. При этом принималось, что машина изолирована и вследствие этого изменение состояний происходит только в силу внутренней деятель-ности машины. Теперь мы рассмотрим, что происходит с разнообразием, когда система является машиной со входом.

Рассмотрим для начала простейший случай, когда машина имеет один параметр Р, изменяющийся через большие промежутки времени. Положим для ясности, что машина имеет множество копий, тождественных по своим преобразованиям, но различающихся состояниями, в которых они находятся. Предположим, что мы наблюдаем множество состояний, обнаруживаемых в каждый момент множеством машин. Пусть Р имеет одно и то же значение для всех машин и сохраняет его, в то время как машины изменяются шаг за шагом. Условия здесь те же самые, что и в предшествующем параграфе; и если мы измерим разнообразие состояний для множества копий и будем наблюдать, как оно изменяется со временем, то мы увидим, что оно упадет до определенного минимума. Когда разнообразие достигнет своего минимума при данном входном значении Р\, пусть Р примет некоторое новое значение Р2 одновременно и одинаково для всего множества копий.

Изменение входного значения переведет график машины из одной формы в другую, например (если машина имеет состояния А, В, , , ., F), из

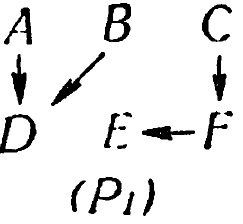в

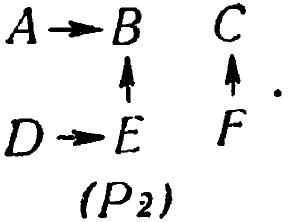При Р1 все машины, находившиеся в A, B или D, перейдут в D, а находившиеся вначале в С, Е или F перейдут в Е. Через некоторое время при Р1 разнообразие упадет до двух состояний. Когда Р примет значение Р2, все те системы, которые находятся в состоянии D, перейдут за первый шаг в Е (поскольку преобразование однозначно), а все те, которые находятся в E, перейдут в В. Легко видеть, что когда изменение одинаково для всех систем, изменение значения параметра во всем множестве не может увеличить разнообразия этого множества. Это, конечно, истинно независимо от того, являются ли D и Е состояниями равновесия. Пусть теперь система продолжает действовать при Р2. Обе группы систем, первоначально (после первого шага) находившиеся в различных состояних (D и E), перейдут в В; теперь они все будут находиться в одном и том же состоянии и разнообразие упадет до нуля.

Таким образом, изменение значения параметра делает возможным уменьшение разнообразия до нового, более низкого минимума.

Очевидно, что переход Р1 Р2 может привести к дальнейшему уменьшению разнообразия при том условии, что два или более состояния равновесия для Р1 лежат в одном и том же бассейне Р2 .Поскольку это случается часто, мы можем высказать менее строгое, но более наглядное положение: единообразное изменение входов некоторого множества преобразователей имеет тенденцию уменьшать разнообразие этого множества.

По мере уменьшения разнообразия множество изменяется так, что все его элементы имеют тенденцию в каждый момент находиться в одном и том же состоянии. Другими словами, изменения входа некоторого преобразователя имеют тенденцию ослаблять зависимость состояния системы (в данный момент) от индивидуального начального состояния преобразователя и усиливать зависимость состояния системы от той последовательности значений параметра, которая применялась на входе.

Этот же самый факт можно рассмотреть и с другой точки зрения. В изложенном выше рассуждении за <множество> принималось, для ясности, множество одновременно действующих копий одного и того же преобразователя. Но наша теорема одинаково применима и к одному преобразователю, взятому в различных случаях, если различные начальные моменты приведены в должное соответствие.

Эта точка зрения была бы более подходящей, если бы мы исследовали какой-нибудь очень сложный преобразователь, предпринимая на нем ежедневно новые эксперименты. Если бы он содержал большое количество практически недоступных частей, то было бы, возможно, трудно возвращать его каждое утро в некоторое стандартное состояние, готовое для следующего эксперимента. Наша теорема утверждает: если вход преобразователя рано утром проводить через некоторую стандартную последовательность значений, то чем длиннее эта последовательность, тем более уверенно можно сказать, что машина будет приведена в некоторое стандартное состояние, готовое для эксперимента. Экспериментатор, может быть, не сумеет назвать это состояние, но он может быть уверен, что оно имеет тенденцию быть воспроизводимым.

Следует отметить, что недостаточно простого равенства значений параметра на каждом шаге данной последовательности. Чтобы результат был не просто номинальным (т. е. недействительным), параметры должны испытать фактическое, т. е. ненулевое изменение.

Истинность этой теоремы ни в коей мере не зависит от размеров системы. Очень большие системы подчиняются ей так же, как и малые, и часто можно даже ожидать, что они обнаружат соответствующее поведение более плавно и регулярно (в силу статистического эффекта больших размеров). Поэтому теорему можно с успехом применять к мозгу и к социально-экономическим системам.

Примеры, соответствующие этому процессу, весьма обычны. Возможно, нечто в этом роде имеет место, когда мальчики, обладающие явно выраженной индивидуальностью, приобретают по окончании одной и той же школы привычки, более характерные для школы, которую они посещали, чем для их собственных первоначальных индивидуальностей. Выяснение того, до какой степени эта тенденция к однообразию поведения связана с рассмотренным свойством преобразователей, следует предоставить дальнейшим исследованиям.

Необходимо дать, этому явлению имя, на которое мы могли бы впоследствии ссылаться. Я буду называть его законом накопления опыта. Более наглядно его можно было бы описать, сказав> что информация, связанная с изменением параметра, имеет тенденцию разрушать и замещать информацию о начальном состоянии системы.