7/13. Степени свободы. Если некоторое множество векторов не охватывает всех возможных значений ( 7/11), то остающуюся еще свободной область иногда можно успешно измерить, указав, сколько независимых соста-вляющих дали бы такое же разнообразие. Это число составляющих называется степенями свободы данного множества векторов. Так, огни светофора ( 7/8) имеют разнообразие, равное четырем. Если составляющие по- прежнему будут принимать каждая по два значения, то две составляющие смогут дать то же самое разнообразие (четыре). Таким образом, можно выразить ограничение разнообразия светофора, сказав, что три взаимозависимые составляющие дают такое же разнообразие, какое давали бы две независимые составляющие; т. е. три огня имеют две степени свободы.

Если возможны все комбинации, то число степеней свободы равно числу составляющих. Если возможна только одна комбинация, то число степеней свободы равно нулю.

Необходимо иметь в виду следующее обстоятельство. Этот способ измерения того, что остается свободным от ограничений разнообразия, применим лишь в некоторых благоприятных случаях. Так, если бы огни светофора допускали три или пять комбинаций, то эквивалент не выражался бы так просто - целым числом. Это понятие имеет значение главным образом тогда, когда составляющие изменяются непрерывно, так что каждая может иметь бесконечное число значений. Подсчет с помощью степеней свободы нередко возможен и в этом случае, хотя состояния не могут быть сосчитаны.

Упр. 1. Если торговец подержанными автомобилями хвастает, что его запас покрывает область 10 возрастов, 8 мощностей и 12 цветов во всех возможных комбинациях, то сколько степеней свободы имеет его запас?

Упр. 2. Двумя составляющими вектора являются угловые положения двух стрелок на часах. Имеет ли множество векторов (на интервале в 12 часов) ограничение разнообразия, если углы измеряются точно?

Упр. 3. (Продолжение.) Сколько степеней свободы имеет этот вектор? (Указание: вызовет ли отсутствие минутной стрелки существенную потерю?)

Упр. 4. Изменение направления осей двух движущихся глаз определяет вектор с четырьмя составляющими: верхнее и боковое отклонения правого и левого глаза. Человек обладает бинокулярным зрением; хамелеон двигает глазами независимо, причем каждый глаз отыскивает пищу на своей стороне тела. Сколько степеней свободы имеют глаза хамелеона? Глаза человека?

Упр. 5. Стрела заданной длины, лежащая на плоскости, имеет три степени свободы (две координаты определяют, скажем, положение ее центра, а один угол определяет ее направление). Сколько степеней свободы будет у нее, если добавить ограничение, что она должна всегда указывать в направлении данной точки Р?

Упр. 6. Т есть некоторое замкнутое однозначное преобразование, а a - любой из его операндов. Рассмотрим множество векторов, имеющих каждый по три составляющие,

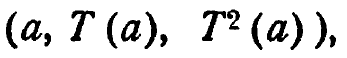
где а принимает поочередно все свои возможные значения. Сколько степеней свободы имеет это множество?

Упр. 7. Каким образом обычный график зависимости у от х обнаруживает ограничение разнообразия?

Упр. 8. Сколько степеней свободы имеет обычное тело, например стул, в трехмерном пространстве?