13/15. Эта особенность проектирования - сведение многих начальных возможностей к одной или нескольким конечным - легко поддается измерению. Мы можем использовать здесь ту же меру, что для разнообразия и для информации, которые измерялись либо непосредственно, либо логарифмически ( 7/7 и 9/11).

Эта мера удобна и, кроме того, определяет естественным образом ту пропускную способность, которую должен иметь канал С в системе

чтобы была возможна передача необходимого разнообразия или информации от проектировщика к машине.

Заметим, что этот метод не дает никакого ответа на вопрос: "Какое количество проектирования имеется в данной машине (без указания на то, чем она могла бы быть)?" в данной машине (без указания на то, чем она могла бы быть)? Ведь наша мера существует лишь для множества возможностей. Она относится не к полученной вещи, а к акту передачи сообщения ( 13/11).

Приводимые ниже упражнения помогут придать реальность этим несколько абстрактным рассуждениям и покажут, что наши рассуждения достаточно согласуются с тем, что интуитивно очевидно.

Упр. 1. На одном из этапов проектирования некоторой электрической машины надо определить значения трех различных омических сопротивлений. Каждое из них может независимо иметь одно из 7 значений: 10, 15, 22, 33, 47, 67 или 100 ом. Какое количество разнообразия должен обеспечить со своей стороны проектировщик (согласно закону необхо-димого разнообразия), чтобы свести все возможности к одной?

Упр. 2. (Продолжение.) Значения трех сопротивлений выбираются из множества: 10, 11, 12 ... 99, 100 ом. Какое разнообразие должен обеспечить со своей стороны проектировщик?

Упр. 3. Каждое из трех сопротивлений должно иметь значение 10, 20 или 30 ом. Если они соединяются параллельно, то какое разнообразие должен обеспечить со своей стороны проектировщик, чтобы свести разнообразие возможных электричек ских свойств к одному свойству?

Упр. 4. Сколько нужно проектирования для выбора между двумя машинами с состояниями a, b, с и d:

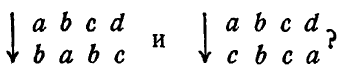
Упр. 5. Сколько проектирования требует изготовление монетного штампа для пенсов, если этот штамп рассматривается: (I) как состоящий из 15000 точек, каждая из которых может иметь любую из 10 возможных интенсивностей; (II) как окончательная форма, выбираемая ее величеством королевой Англии из трех представленных форм? Объясните несовпадение ответов.

Упр. 6. Сколько разнообразия требуется для сведения к одной машине всех возможных машин с n данными состояниями? (Указание: упр. 7/7/8.)

Упр. 7. (Продолжение.) То же самое, но число состояний машины равно n, а число состояний входа после проектирования равно i.