2/4:  1. Нет. 2. Нет. 3. А -да, В-да, С -нет, D -да.
4. Оно должно иметь вид аа. 5. Да; матовая позиция не может иметь образ, ибо правила не разрешают дальнейших ходов; если преобразование мистера С замкнуто, то каждая позиция, к которой приводит его ход, может смениться другой, так что его преобразование не может содержать ходов, ведущих к мату.

2/5:  1. Да. 2. Нет; некоторые операнды, например 40, кончаются на 0 и будут преобразованы в 0, который не входит в множество операндов.

2/6:  1. n' = n + 10 (n = 1,2,3) 2. а) n'= 7n (n= 1, 2,3 для всех преобразований); b) n'= ; с) n'= 1/n; d) n' = 11 - n; е) n'= 1; f) n'= n.

5. Да. 6. Да.

2/8. 1. Однозначно лишь в одну сторону: и 1, и 8 переходят в 9.

2/9:  1. <Нет выручки> . 2. Сухая игра.

2/10: 1. На главной диагонали стоят только +, на остальных местах-нули. 2. а) (II); b) (III); с) (I). 3. а) Да. b) Нет.

4.     Распределения одинаковы; одно есть просто отражение другого. 6. 9 1) - 7. 4.
1) Вот эти матрицы:

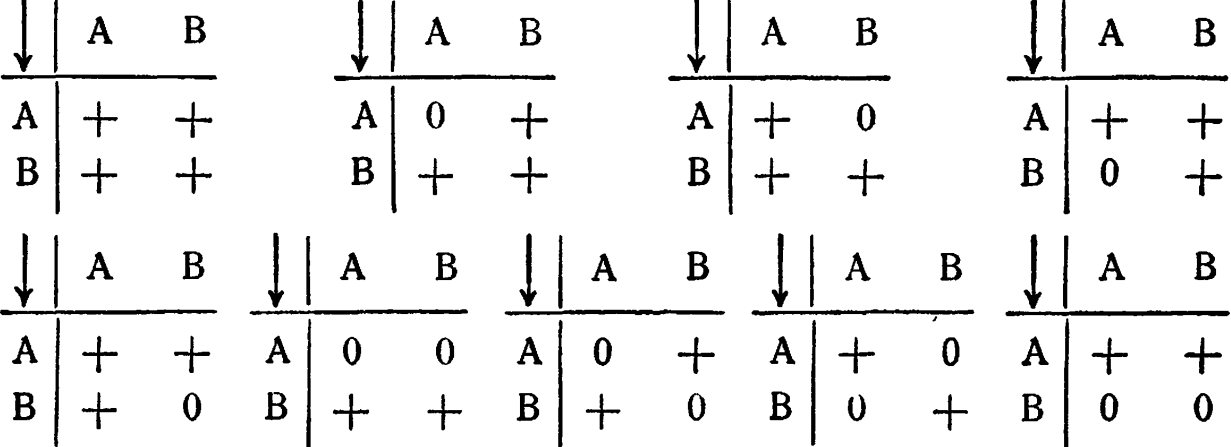
В оригинале в качестве ответа ошибочно указано число 16. (Такое число действительно получится, если допускать столбцы, целиком заполненные нулями, т. е. "операнды, не имеющие образов"). Прим. ред.

2/11:	1.
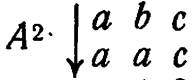	2.	Taков, кaкoвo и caмo npeo6paзoвaниe.
	3.	A.
	4.	n'=n+2 (n= 1,2,...
	5.	n'=49n (n=1,2,...).
	6.

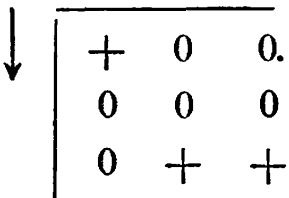2/14: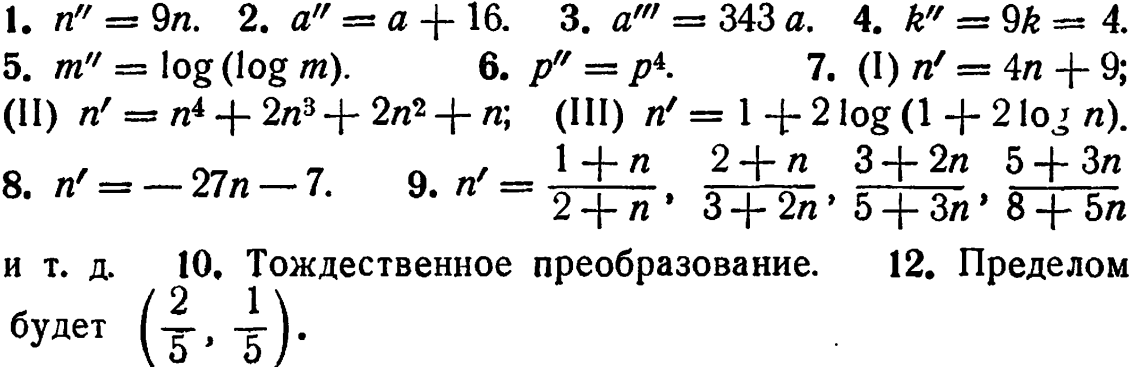

2/15: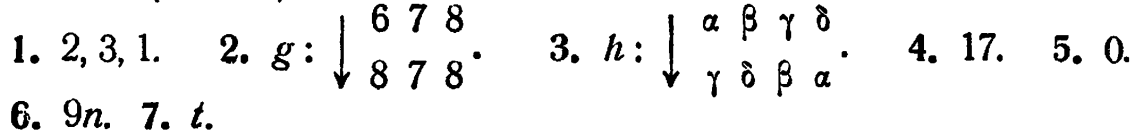

2/16: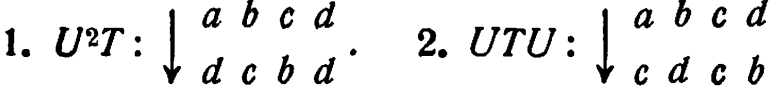

3.     Они тождественны; эта эквивалентность является главным оправданием того, что преобразования выписываются сверху вниз, а не слева направо (ср. упр. 9/6/8 и 12/8/4).

2/17: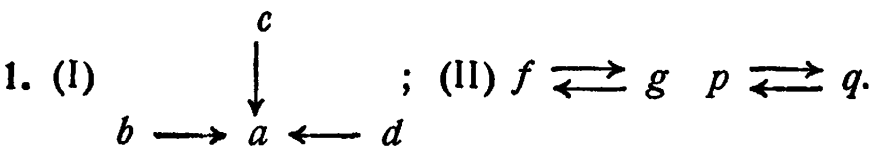
	2.     В нем нет стрелок, а только изолированные точки.
	3 Они состоят только из изолированных точек и (или) простых колец без разветвлений.
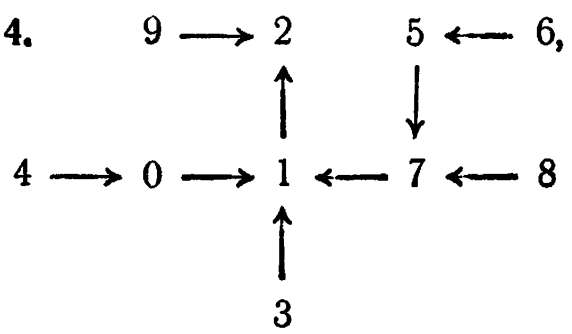	если используются 4-значные логарифмы.
	5. 7, 1, 2, 2.
	6. Нет.
	7.   Да.
	9. Нет.

3/1:  1.     Возможные ответы: (а) яйцо, сваренное всмятку яйцо,сваренное вкрутую; (b) полено зола; (с) цилиндр, полный смеси паров бензина и воздухацилиндр, полный пламени;
(d) одноклеточное яйцо двуклеточное; (е) кучевое облако гроза; (f) течка  беременность; (g) низкие цены (при небольшом запасе товаров) высокие цены; (h) кошка видит мышь  кошка преследует мышь; (i) близкие туманности рассеянные туманности.

3.4   1.     n' = 2n'. 2. 2, 4, 8, 16, 32, . 3. График (II): 1000 2000  4000.... 4. n'= 0,8n. 5. (I) 800, 640, 510,410, 330 X ; (II) к нулю. 6. Она придет к состоянию 3 в котором и останется; 3 - единственное состояние, в котором она может остановиться. 7. Она придет к циклу из состояний 2 и 8, между которыми и будет без конца колебаться. 8. Четыре: два с состояниями равновесия и два с циклами. 9. n'= 0,9n + 1 000 000. 10. 20; 19; 18; 1; .  11. 10 000 000. 12. Если l - его длина, то изменение его длины за единицу времени будет равно l' - l; следовательно,l' - l=1,2, и преобразование будет иметь вид l'=l + 1,2. 13. Увеличение числа бактерий (но не их новая численность!) равняется n' - n; следовательно, ,
и преобразование имеет вид .

14. 19,.

3/5: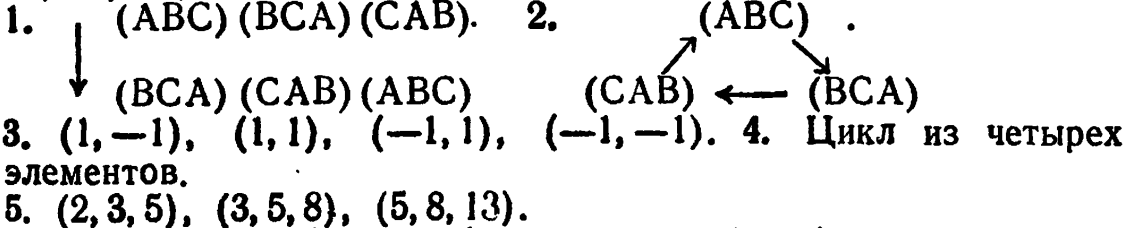 

3.6:
1.     (1/2,2), (2,-1/2); (-1/2,-2),(-2,1/2), (1/2,2) и т.д.
2.     (1,2,0,2,2). ,4. Добавятся не связанные друг с другом новые циклы, из двух элементов каждый. 5. (8,-3, 1). 6. (8, 4) преобразуется в (6,6), и система остановится. 7. Если операнд обозначить через (а, b),то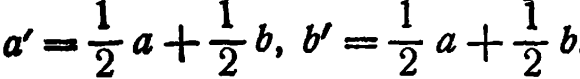

8. (30,34) (28,36) (24,40) (16,48)  (0,64)  ?. Нельзя определить, что произойдет дальше, если не решено, можно ли занимать деньги.

9. .

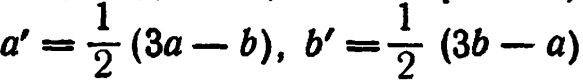10. Тот, кто начнет с большим количеством денег. 11. m' = m - n, n' = 2n. 12. Вектор (m, n). 13. (150, 10) (140, 20) ... (0, 160), после чего алгебраические изменения более не соответствуют зоологическим. 14. х = 10, 0, -5, -5, -2 1/2, 0, 1 1/4, 1 1/4, 5/8; нет. 15. Он сильно демпфирован. 16. Цели х - заработная плата, а у - индекс цен, то первое утверждение означает, что х' - х = у-100, а второе означает, что у' = х; следовательно, преобразование будет иметь вид x' = x + у-100, y' = х. 17. (110, 110) (120, 110) (130, 120) ...  (1540, 990). 18. Нет, система описывает <порочную спираль> . 19.(110, 110) (110, 100) ...(100 5/16, 100 5/16). 20. Обе кривые сходятся к 100. 21. Вторая система устойчива; первая обнаруживает самовозрастающую инфляцию. 22. (80, 120) (100, 80) (90, 110) ...   (99 3/8, 100 5/8). 24. Да. 25. 3.

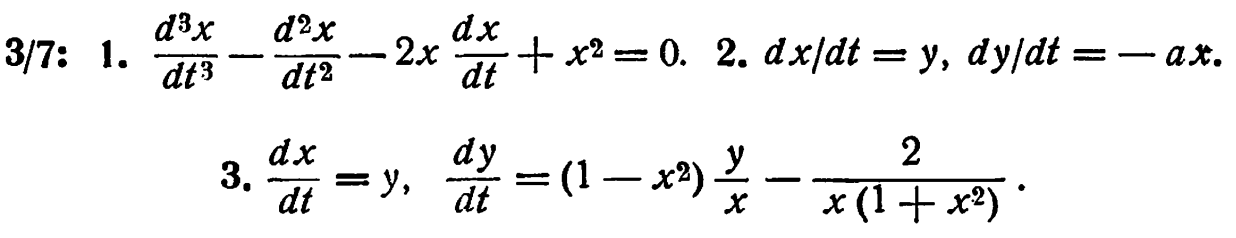
4/1: 1. Три. 2. Да. 3. Под действием R1 она пройдет с d b; затем под действием fa она пройдет b а b; следовательно, она окажется в b. 4. (I)R1 и затем R2;  (II) R1, R3, R2.
5.     Получится преобразование х' = 4, у' = 4 - у; заметим, что уравнение в первой строке, относящееся к х, стало теперь неверным: фиксация переменной заставляет машину изменить поведение. 6. В каждом столбце все состояния должны быть одинаковыми.

4/2: 1.(I) g' = 2g - 2h, h' = 2g - 2h; (II) g' = g-h, h' = 2g; (III) g' = 0, h' = 2g + 2h. 2. (I) h' = j, j' = e-h; (II) h' = log (2 +sin h), j'=1 + sinj. 3. (I) 0; (II) 2; (III) noneременно 1 или 2; (IV) a = 1 для 90 шагов, а затем a = 10. 5.    PV = 10; да, приблизительно. 6. n' = n + a2. 7. Да; каждый скачок равен n' - п, а это равно 3a.

4/3:
1.     аb = 00    01    10    11    20    21
s' = s       s      0      t       - s    - s + 2t
t' = t         2t     t - 1  2t     t - 2  2t
2.     3. 3. a = 9/8, b=1,8. 4. a = 9/10, b = -1/10. 5. Четыре (ab = 0, 1, 2 или 4).

4/4: 1. Это соответствует тому, что а и b становятся и остаются равными, т. е. тому, что преобразование принимает вид
p' = a(p + q). Q' = a(p + q).

4/5:  1. График должен состоять из одной-единственной цепи, соединяющей все состояния. 2. Последовательность (8, 4), (6.6).

4/7:  1 и 2 (скобки опущены). График имеет вид

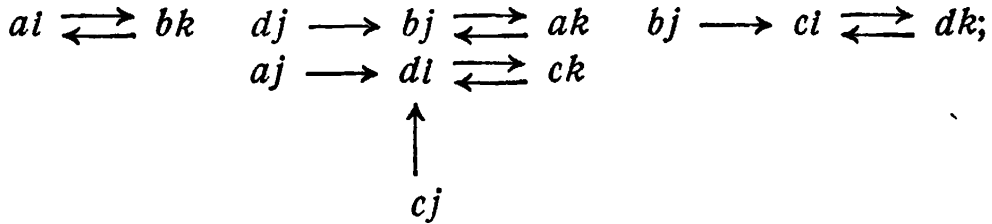
он содержит четыре бассейна.

4. Да. 5. n1n2. 6. . 7. Каждая часть последовательно перейдет в состояние 0. 8. Изменение ... 0, 0, 1, 2, 0, 0 ... произойдет в каждой части по очереди, напоминая прохождение импульса по нерву.

3.     Сделать в X все значения Р одинаковыми.

4/9:  1. р, q; г, s, t, u. 2. (1, 0, 1, 0, 0).
4/11: 1. 6 между шестью парами, такими, как AB; 8 в четырех тройках, таких, как АВС (в обоих направлениях); и 6 между всеми четырьмя (ABCD; ABDC; ACBD; ACDB;ADBC; ADCB). 2. х'= у + z, y' = 2z, z' = x - 1. 3. Да; в этом случае преобразование будет иметь вид
x' = y + z, y' = 2z, z' = х- 1.
4.     Да.
4/12:        1. (Квадратики опущены для простоты): (I) ух (у доминирует над х); (II) 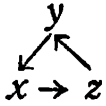(система с обратной связью); (III) ( <целое> фактически состоит из двух несвязанных частей); (IV) u х  у z (цепочка действий);

у равно нулю.
4/13:        1. z доминирует над х, а у не зависит от обоих.
4/14:        1. Только (III).
4/15:        1. Если переменные суть: S = Пение, L = Смех, X - игра на органе, Y = сожжение ладана - и если каждая переменная принимает значения 0 или 1, обозначающие соответственно бездействие или действие, то легко найти машину со входом

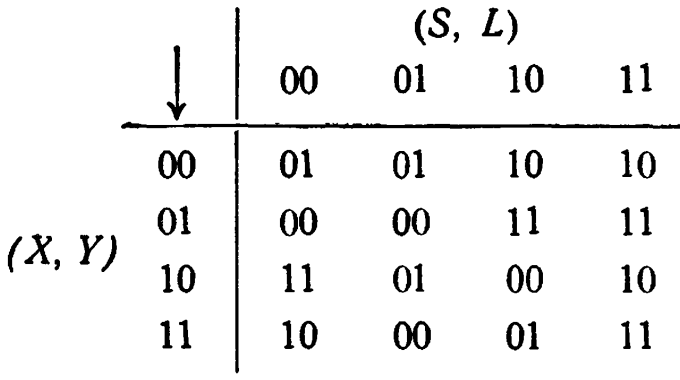
Один из путей к (0, 0) таков: прекратите ровно на одну минуту сжигать ладан; затем, не зажигая ладана, играйте на органе; затем перестаньте играть и зажгите ладан; в будущем все время жгите ладан и никогда не играйте на органе. 2. Да, ибо значения S влияют на переходы L. 3. Нет.

4/19: 1. Один из возможных способов - бросать кость, чтобы выпадающие числа определяли последовательно образы для S1, S2 и т. д. 2. Один из возможных способов - перенумеровать шесть карт от 1 до. 6, перетасовать и расположить их в ряд, а затем в том же порядке вписать состояния в ниж-нюю строку преобразования. 5. См. 4/20.
4/20: 1. Да, нет, нет.
5/3: 2. Нет. 3. Единственное состояние равновесия есть (0, 0). 4. Все точки на оси у - равновесные. 5. j = 0, k = -1. 6. Да. 7. Нет. 8. Каждая стрелка возвращается в то же состояние, из которого вышла, так что представляющая точка неподвижна. 9. Тождественное преобразование. 10. Да. 11. Да.
5/4: 1. Таково, например,

	a	b	c	d	e	f	g
	b	a	d	c	e	f	g

3. Нет. 4. Нет. 5. Нет. 6.        Каждая траектория есть цикл. 7. Нет.

5/5: 1. Только b+ с+ g. 2. Да. 3. Да. 4. Да.
5/6:  1. Да; последовательность D(c), TD(c), T2D(c), T3D(c),:будет иметь вид d, а, с, с.,,, 2. Нет; пределом является не е. З. Система, хотя и будет выведена из данного множества, всегда вернется в него.
5/7: 1. Одно из возможных множеств преобразований

	а	b	с	d
T	а	b	а	b
D	с	с	.	.
Е	b	d	.	.

5/9: 1. а = (100, 100); D превращает его в (110, 110), т. е. = 10, = 10; Т дано; система неустойчива. 2. а и D таковы, как раньше, но Т изменилось, и система стала устойчивой. 3. Как правило, пределом будет не а, а какое-либо другое состояние; система неустойчива относительно таких D. 4. Да; отклонения стремятся к нулю, который является состоянием равновесия.
5.     Нет; отклонения увеличиваются, причем это увеличение ограничено лишь посторонними факторами, такими, как форма соединительных звеньев.
6. Чтобы отклонения уменьшались, а не возрастали.
7. Самовозрастающими; и это постоянный источник головной боли для организаторов движения.
8. Каждое отклонение от состояния равновесия увеличивалось бы, пока не вступил бы в действие какой-нибудь другой ограничивающий фактор.
9. Да; для всех смещений D;так, если D перемещает состояние в , то последовательные значения х суть 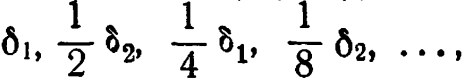, что, очевидно, сходится к 0; то же самое для у.

5/13: 1. Нет, ибо в этом случае у должен будет иметь состояние равновесия 0 при каком-то значении , т. е. должна удовлетворять уравнению 0 = 20 + 3, что невозможно.

6/3:  1.     См. 6/5.

(протокол не дает никаких данных о переходах из g при входе ). 3. Нет, так как переход
от С не однозначен. 4. Да, насколько можно судить по имеющимся данным 5.      
(х, у) 00 01 02 10 11 12 20 21 22.
(х', у')  01 00 11 11 00 21 11 20 11
6.     Для каждого входного значения должны наблюдаться n переходов, что отнимет по крайней мере n шагов: следовательно, для наблюдения всего множества преобразований требуется по крайней мере mn шагов. 7. Выберите любые два значения для x и ? и посмотрите, каким будет значение х'. Так, равенства = 1, х = 4, х'= 4 покажут, что мы имеем дело с ящиком 1. Еще более простой способ - положить = 0 и посмотреть, будет ли значение х увеличиваться или уменьшаться.
6/7: 1. у доминирует над х.

6/9: 1.

	a	b	c	d	e
	t	p	r	q	s

2. Три 1). 3. Необходимы две переменные: показание циферблата (v) и скорость изменения этих показаний . Тогда для верхней системы получим dv/dt = ,, где k представляет упругость пружины и момент инерции массы, a f - коэффициент трения. Для нижней системы получим
1) Вот эти преобразования:

a b c p r q

,

a b c r q p

,

a b c q p r

 (в оригинале в ответе ошибочно написано: <шесть> ). - Прим, ред.
Чтобы быть, изоморфными в строгом смысле, определенном выше, системы должны иметь f = R/L и k=1/CL. Если это так, то их изоморфизм может быть показан при помощи взаимного однозначного преобразования

6/10: 1. Они тождественны:

2. (II) и (IV) могут измениться; (I), (III) и (V) не изменятся. 3. Они не изменятся.

6/11: 1. Предположите, что х - цена масла, а у - цена сахара; их разница сегодня равна х - у; их разница завтра будет (х- у)'; а это есть то же самое, что завтрашняя цена масла минус завтрашняя цена сахара, т. е. х'- у'.
6/12:        1. Да, если рассматривать взаимно однозначное преобразование просто как предельный случай преобразования, однозначного лишь в одну сторону.
6/13:        1. Четное + четное = четное, Ч + Н = H, Н + Ч = Н, Н + Н = Ч         2. (Пусть <х + у> "x и y" означает: "слить x и y"). Имеем системы: (I) а + b;     (II) c + d;

(III) а + b и c+d; (IV) b + c + d;  (V)  a + b + c + d; (VI) (для полноты картины) первоначальная система, где ничто не слито. 3. Можно слить состояния (х, у) и (-х, у), ибо изменение знака их не меняет следующего состояния (х', у'),        следовательно, сказать, что настоящее состояние есть (+4, -2), без уточнения знака х, достаточно для того, чтобы показать, что следующее состояние будет единственно и равно (+2, +14).

6/16: 1. Система неотличима от модели. 2. Она существует, как и мозг; они изоморфны на низшем уровне. 3. (I) a, b + c + d изоморфно р, q + г;

(II) а + b     + c + d изоморфно p + q + r.

7/6: 1. 26-26-26, т. е. 17576. 2. 16. 3. 11. 4. 2.2.2 ... десять раз, т. е. 1024. 5. 5x должно быть не меньше 2 109, следовательно, беря логарифмы по любому удобному основанию (например, десятичные), получим xlg5 lg2 + 9lg10, или x(lg2 + 9 lg 10)/lg 5 13.3;
это значит, что необходимо по крайней мере 14 таких процедур.
6.     (I) 27; (II) 21. 7. 27. 8. = 27 и = 81. Значит, чтобы отобрать 1 из 52, нужно четыре указания. 9. 3, ибо группа отца может быть О, или А, или В1).
7/7: 1. Один бит. 2. (I) 2,32 бита; (II) 30,9 бита. 3. 4,7 бита.
4.     5?4,7 = 23,5 бита. 5. (I) I бит, (II) 20 битов. 6. , т. е. 1 048 576. 7. Замещение каждого вопросительного знака имеет разнообразие 6log26 битов, так что целое имеет разнообразие 6 log2 6 битов, т. е. 15,5 бита. 8. nlog2n битов. 9. 12 000 битов. 10. Страница в 5000 слов может нести около 50 000 битов - больше, чем запись. 11. При прочих равных условиях разнообразия также равны. 12. Множество "всех возможных брошюр, напечатанных на
1) Ср. Hirszfeld L., Les groupes sanguins, Paris, 1938, p. 74. В оригинале в ответе ошибочно написано: <Нулевое многообразие> . - Прим, перев,
английском языке и занимающих при чтении 10 минут>. Разнообразие принадлежит не брошюрам, а этому множеству. 13. Конечно, оно должно только отличаться от других возможностей.
7/12: 1. Нет, ибо исчерпаны все комбинации прошлых и нынешних семейных положений. 2. Да; отсутствует 4 возможности.
7/13:        1. Три, поскольку речь идет об упомянутых количествах. 2.        Да, если стрелки поставлены аккуратно; так, если часовая стрелка стоит точно посредине меж двух цифр, то минутная стрелка обязательно показывает <полчаса> . 3. Одну, ибо информация, даваемая минутной стрелкой, вытекает из инфор-мации, которую дает часовая стрелка. 4. Глаза хамелеона - четыре, глаза человека - немногим больше двух, ибо могут двигаться с некоторой небольшой независимостью. 5. Две. 6. Одну, ибо его разнообразие не может превышать разнообразия а; это не зависит от числа составляющих вектора. 7. До проведения графика переменная у могла для каждого значения х иметь любое из своих значений, но после проведения графика переменная у для каждого х может принимать только одно значение. 8. Шесть.
7/15: 1. Он говорит, что числа, выражающие отношения веществ в химических соединениях, образуют небольшое (имеющее, быть может, лишь несколько десятков членов) подмножество множества всех рациональных чисел (количество которых бесконечно). 2. Из всех геометрически возможных траекторий, из всех тепловых изменений и пр. он допускает лишь немногие.
7/19: 1. Из возможных переходов, например а > а, а > b, a > c исключаются все, кроме одного, ибо переход от а должен быть однозначным; аналогично для b и т. д.
7/20: 1. 8. 2. 17. 3. 12. 4. (I) 1 048 576; (II) 21 892.
7/22: 2. Разнообразие паразитов: очевидно, что некоторый вид может служить хозяином нескольким видам паразитов. 3. V однозначно в одну сторону и вызывает снижение разнообразия. 4. Что ему не хватает способности различения. 5. (I) 6 состояний; (II) 2 состояния. <Ванна не в порядке> . 6. Вероятность того, что данное состояние Si будет образом состояния Sk, равна 1/п. Вероятность того, что Si не будет образом Sj, равна 1-1/n. Вероятность того, что Si не будет образом состояния Sk, также равна 1-1/n. Следовательно, вероятность того, что Si не будет образом никакого состояния, равна (1- 1/n)n. Это даст нам долю операндов, которые исчезнут после преобразования. Если n стремится к бесконечности, то эта доля стремится к 1/е. Следовательно, остающаяся доля, которой принадлежит разнообразие, стремится к 1-1/е.

7/24:        1. 3 состояния = 1,58 бита. 2. Еще на 1,58 бита. 3. становятся последовательно 5а, 5а + 7, 10а + 14, 10а + b + 14. Если вычесть 14, то останется 10а + b. Так, сто сочетаний а и b (если допускается 0 и 0) преобразуются взаимно однозначно после вычитания 14 в сто чисел от 0 до 99. Разнообразие равно 100 состояниям, или 6,64 бита. 4. Для всех сочетаний двух одноразрядных чисел, которые предлагаются в подобных случаях. 5. Нулевое. 6. 2 состояния, 1 бит; либо разные цепи, либо одна и та же цепь в разные моменты времени. 7. Нет. Они могут вместе проходить один и тот же цикл. Различайте: (I) тождественность состояний, занимаемых разными машинами в один и тот же момент, и (II) тождественность состояний одной машины в разные моменты времени.
8/3: 1. Не больше, чем за одно снятие.
8/4: 1. Да; <взять антилогарифм> . 2. Нет; различные значения х могут дать одно и то же значение х'. 3. Тождественное преобразование. 4. n' = n - 7. 5. х' = х - у, у'= -х + 2у. 6. 3log2 26 битов, т. е. 14,1 бита. 7. 263= 17 576. 8. Iog28 + log27 = 5,8 бита. 9. (Для английского алфавита) нет: разнообразие будет 5,7 бита, а этого недостаточно (log2 52 < log2 56). 10. 1 бит; сообщений два: <ухаживает> и <не ухаживает> . Сложность молекулы гормона и обряда <ухаживания> здесь не имеет значений.
8/5: 1. A A C B D D B C B C C B. 2. a c d b d c d. 3. b d c d b a d. 4. Да. 5.        10, 8, 7, 10, 11, 9, 8. 6. 10, 8, 4, 3, -1, -1, 3, 0, 1, 1, - 1,.... 7.      х - 2, 1, 2, -11, 11, -2, 16 ..., а у = 1, 4, -11, 13, -21,-13, -93, .... 8. х = exp (-4t - sin t). 9. х = 1/2 (е-t + te-t - cost). 10. х преследует а и приближается к нему все ближе и ближе.
8/6: 1. Нет, в таблице преобразований должно быть 108 строк, так что каждый столбец должен содержать 108 элементов; а их имеется всего 100, так что будут повторения. 2. (I) 7, (II) 512. 3. Присоединению прибора, такого, как спидометр или тахометр, который выдавал бы число, пропорциональное производной по времени. 4. Нет; ибо если выход постоянно равен нулю (как будет в случае, если он начнет с нуля), то значение а нельзя вывести из переходов х, которые будут 0>0 для всех а.
8/7: 1. Он не сохраняет всех различий, поэтому для него принципиально невозможно создать совершенный обратный преобразователь.
2.     (b, В)       R R R
(Ь, С)       S S S
(b, D)       (не встретится)
(с, А)       S S S
(с, В)       R R R
(с. С)       (не встретится)
(с, D)       Q Q Q
(d, А)       (не встретится)
(d, В)       Q Q Q
(d, С)       R R R
[d, D)       S S S
3.     Его диаграмма непосредственных воздействий должна быть u>х>у, где у выдает значения и на два шага позже. х может иметь вид

	x1	x2	x3	...
u1	x1	x1	x1
u2	x2	x2	x2
u3	x3	x3	x3
...	и т.д.

       

 

Если теперь у имеет вид

	U1	U2	U3	...
x1	U1	U1	U1
x2	U2	U2	U2
x3	U3	U3	U3
...	и т.д.

то у будет выдавать заглавные буквы, соответствующие первоначальным значениям u.
Если рассматривать (х + у) как одну машину с состояниями (х, у), то преобразование будет таким:
Вообще, ui переводит (xj, Uk) в (xi, Uj), которое переходит на следующем шаге в (-, Ui), повторяя таким образом первоначальное ui.
8/8: 1. р' = n, m' = c/d; соедините, положив d = n, с = p. 2. р' = n, m' =1/2 (d - с) + 2; соедините, положив d = n, с = р. 3. P'1 = x, p'2 = y, m'1 = (c1 + c )/2d1, m'2 = (с2 - c1)/2d2; соедините, положив d1 = x, d2 = у, c1 = p1, c2 = p2. 4. Уравнение не может быть решено отдельно для а и b другими словами, а и b влияют на уравнение только в сочетании а + b другими словами, их отдельные воздействия не проявляются раздельно на выходе и поэтому не могут быть прослежены в обратном направлении; все это разные способы выражения одной основной идеи. Заметим, что причина этой невозможности заключается не в отсутствии соответствующих приспособлений, но в том обстоятельстве, что выход не определяет входа; необходимая информация попросту отсутствует.
5.     Для обратного преобразователя требуются спидометры,дающие на выходе и . Тогда любая машина, образующая функции

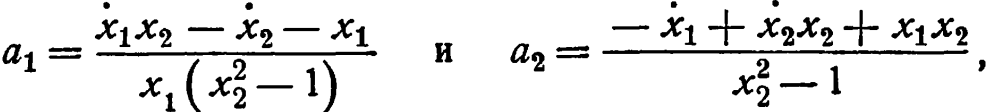
будет выдавать первоначальный вход. Если требуется конкретное преобразование, то [если обозначить функции от и т. д. (см. выше) через A1 и А2] преобразование

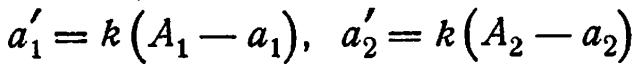
обеспечит сколь угодно близкое приближение к требуемому поведению; надо только, чтобы k было положительно и достаточно велико (упр. 8/5/10). 6. -2 не имеет определенного отношения к (7,3), тогда как 4 имеет, как показало построение таблицы.

8/11:        1. t имеет 3 состояния; u имеет два. 2. t имеет 3 состояния; u не может иметь больше 6, а фактически имеет 5. 3. Т имеет 2 состояния, как и U. 4. 3 состояния: (0, 0, 0, 0), (0. 0, 1, 0) и (0, 1, 0, 1).

8/13: 1. 1 биту на шаг, ибо r имеет только два состояния. 2.   Число различных состояний, занимаемых последовательно, будет для Q: 9, 4, 3, 3, 3; для R: 1, 2, 2, 2, 2; для S: 1, 1,2, 3, 5. 3. В самом деле, скачок от 1 к 4 означает прирост информации, равный 3, тогда как R может обеспечить максимум 2.

8/14: 2. Число взвешиваний при любом способе не может быть меньше трех, ибо передаваемое разнообразие равно log227 битов, а передатчик может нести только log23 битов за шаг.

8/15: 1. Четыре; дольше всего идет передача из А.. 2. Четырех (ответ должен быть таким же, как в упр 8/15/1, ибо эти вопросы по существу тождественны). 3. Три; передача от у самая длинная. 4. Два шага.

8/17:        1. А было в (3,2). [Указание: A'' было в (-1,0), а В" было в (1, 0).] 2. Да; выход позволяет вывести последовательность входных векторов, а последовательность их первых состав-ляющих будет а-сообщением. 3. Нет; движения У суть просто движения А с половинной амплитудой. 4. Если буквы а, b и т. д. обозначают соответствующие движения А, В и т. д. вправо и влево от каких-то нулей по общей шкале, то откуда легко исключить I и n. <Декодирование> соответствует решению этой системы уравнений для а и b как неизвестных через известные y и z.

9/2: 1. Полученное таким образом преобразование детерминированно; как оно получено - не имеет значения. 2. Поскольку каждое состояние должно перейти в какое-то состояние, вероятности и, следовательно, числа в каждом столбце должны в сумме давать 1. 3. Нет. 4. , т. е. 1024. 5. От каждой точки отходит более чем одна стрелка.

9/4: 1. Фактические частоты переходов равны

 

	А	В
А	6	17
В	17	10

Поскольку вероятности в каждом столбце должны в сумме давать 1, первый столбец надо разделить на 23, а второй - на 27. И оценка вероятностей будет

4.

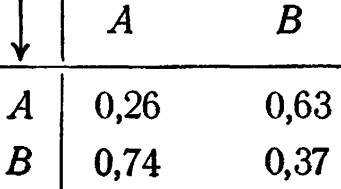
(Эта система фактически использовалась для порождения траектории в упр. 1.)

9/5:  1. Попав под камень, оно бы там и осталось. 2. В должно быть бумагой (где муха прилипает), a D - печкой (где она никогда не остается). 3. От протокола к матрице; протокол дает единственную матрицу, но матрица может дать лишь некоторое множество протоколов. Иначе говоря, потерянная матрица может быть восстановлена по протоколу, но потерянный протокол не может быть восстановлен по матрице.

9/6: 1. (100,0,0), (25,75,0), (62,19,19), (34,61,7) и т. д., с точностью до ближайшей единицы. 3. Грань 3 преимущественно оказывается наверху, грань 4 - внизу; следовательно, грузик спрятан на грани 4. 4. Рассмотрите 100 молекул, и пусть х из 100 молекул А диссоциировали. Игнорируйте молекулы В.
Каждая А имеет два возможных состояния: <диссоциирована> или <нет> - ив каждый промежуток времени имеет следующую вероятность остаться в этом состоянии или измениться:

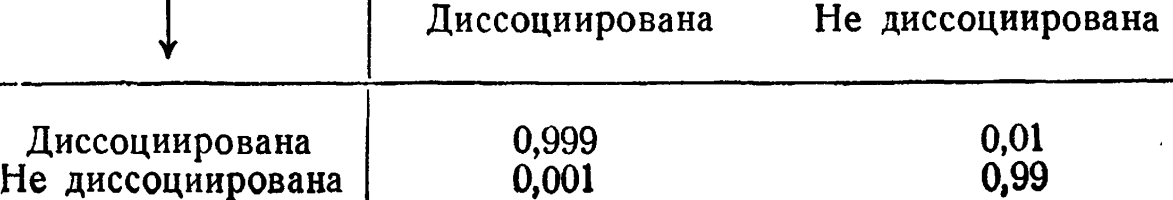
5. Если х и у - числа соответственно диссоциированных и недиссоциированных молекул, то для равновесия необходимы равенства:

х = 0,999х + 0,01 у,

100 = x + у.

Следовательно, х = 90 10/11 . 7. Каждое насекомое может быть в одном из 3 состояний; если имеется n насекомых, то число различных популяций равно
1/2(n + 2) (n + 1).

9/7: 1.     

 

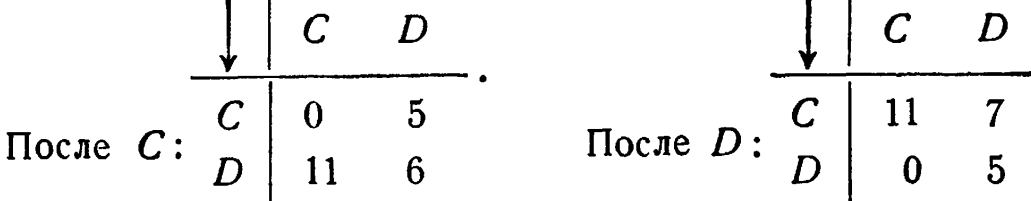
Таким образом, переходы из С явно зависят от того, что стоит перед С.

9/10: 1. 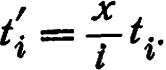   2. Нет. 3. Да 1).
1 См. подстрочное примечание на стр. 247. - Прим. ред.

9/11: 1. Вероятности равны (судя по имеющимся данным) 0,175 и 0,825; следовательно, энтропия равна 0,67 бита. 2. Вероятности равны 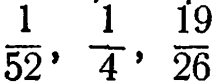следовательно, энтропия равна 0,94 бита. 3. 2,6 бита. 4. 5,2 бита. 5. 2,6 n битов. 6. 0.

9/12: 2. Она всегда будет меньше 1 бита.

9/13:        1. При окончательном равновесии все будут в В и любая последовательность в конце концов будет иметь вид ... ВВВВ... . Здесь нет разнообразия, так что энтропия должна быть равна нулю. 2. Энтропия вычисляется, когда целое находится в окончательном равновесии, а в данном случае окончательное равновесие не допускает предположения, что "система находится в A".

9/16: 1. Да, ибо 62 меньше чем ; = 81, так что может случиться, что хватит 4 сахара, правильно подобранных 2). 2. Все числа в ней одинаковы, как, например, в конце 9/10.

2) Однако может и не найтись таких 4 сахаров среди имеющихся 14. Обозначим значение <кислота> через к и значение <ничего> через н. Допустим, что среди наших 62 видов имеется 6 видов,соответствующие векторы которых таковы:

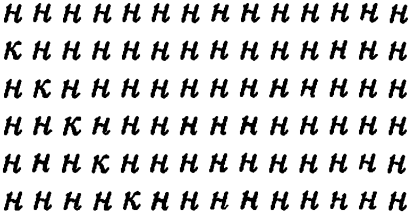
Тогда никаких 4 сахаров (из имеющихся 14) не хватит для различения уже этих 6 видов. - Прим. ред.

9/17: 2. Она должна быть по крайней мере 2000 битов в минуту, если допущения правильны. 3. Каждый палец имеет разнообразие в log2 3 за 1/300 минуты и 300 log23 за 1 минуту, поэтому все 10 пальцев, будучи независимы, имеют 3000 log2 3 битов в минуту; отсюда нижняя граница равна 4800 битам в минуту. 4. 5540 символов в час.

9/18: 1. b может следовать только за а или b, но не за d поэтому Хb должно быть ab,аналогично Хс должно быть ас; наконец, XX должно быть dX.

9/19: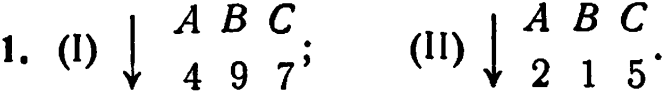        

 2. Только если комбинации и ограничены некоторыми тремя из четырех возможных.

9/20: 1. Искажение, ибо второе обращение восстановит оригинал без потерь. 2. Искажение, если каждое напряжение возбуждает определенную частоту. 3. Порча, ибо различные напряжения определяют одинаковый (нулевой) выход.

9/21:        1. H1 = log29. Энтропия Н2 находится из таблицы:

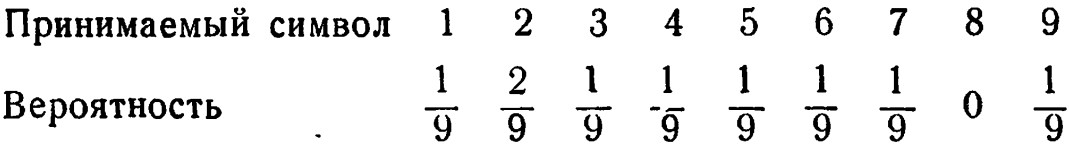
Таким образом, Н2 = 2,948 и, следовательно, ненадежность равна 0,222 бита на символ. 2. Ненадежность = 0; действительно новые сообщения передаются безошибочно. 4. 0,00299. 5. Таблица событий и вероятностей такова:

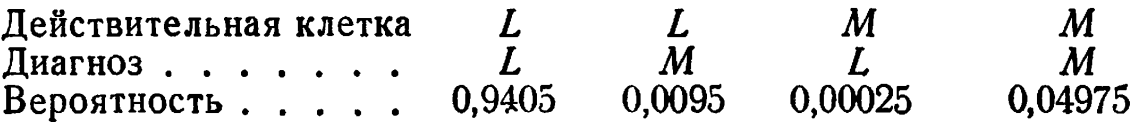
(Проще всего найти вероятности следующим образом: разбить 20 000 клеток сначала на две группы: в 19 000 и в 1000 клеток; затем разбить клетки каждой группы на неправильно определенные клетки и все остальные и, наконец, разделить все количества на 20 000.) Н1 = 0,365 бит/клетка; Н2 = 0,324 бита на клетку. Следовательно, ненадежность равна 0,041 бита на клетку.

10/4: 1. Кошка что-то делает (возможно, играет) с мертвой мышью. 2. Если бы это было возможно, это значило бы, что кошка сделала что-то, в результате чего мертвая мышь ожила!

3. С летально (смертоносно) для М, если ни одно из C(M1), ... . . . , С (Мk) не входит в M1 . . . , Mk.

10/5:        1) Температура и влажность; 2) количество кислорода в крови альпиниста и все, что от этого зависит; 3) направление проходящих внутрь световых лучей; 4) освещенность объектов, которые в противном случае были бы невидимы после захода солнца; 5) температура пищи и, следовательно, степень ее зараженности бактериями; 6) освещенность листьев растения; 7) освещенность сетчатки; 8)    давление (высокой интенсивности) на подошву; 9)        давление при соприкосновении, удерживаемое равным нулю; 10) расстояние между снарядом и целью, которое сохраняется нулевым или маленьким.
11/3:

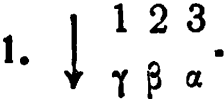
2. Если дано D, то R должно принимать значение, удовлетворяющее уравнению 37 = R - 2D; следовательно, R должно принимать значение 37 + 2D.

3. На главной диагонали ( 2/10) стоят исходы <занос исправляется> "занос исправляется", а на остальных местах - <занос увеличивается> "занос увеличивается ". 4. Нулевое; они все будут с, независимо от разнообразия выборов D. 5. Да.

11/4: 1. Да.

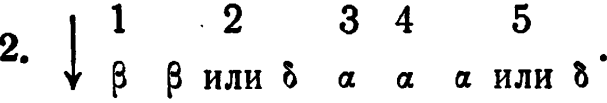
3.     R просто всегда будет выбирать , независимо от хода D.

4.     Да, используя преобразование

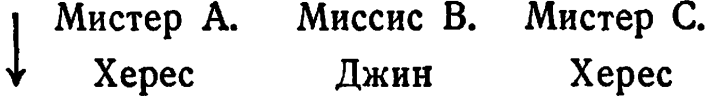
11/11: 1. Да. Разнообразие D равно 10 бит/сек, а зрительный нерв может передавать в 200 раз больше. 2. Пропускная способность, которую можно использовать для регулирования,1 равна 0,63 бит/сек для телеграфа и 5,64 бит/сек для штурвала. Таким образом, нетрудно видеть, что D выдает обычно не более 6,3 бит/сек. 3. Нет, совершенно недостаточна. D дает битов каждый день, а разнообразие, передаваемое генералу, достигает самое большее одной семнадцатой этого. 4. Нет, он может обеспечить только битов в день.

11/14:

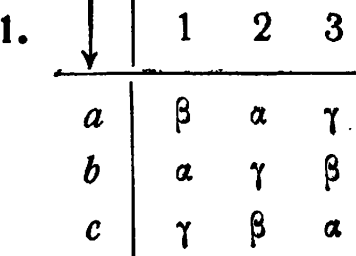
2. D угрожает передавать в Е со скоростью 2 бит/сек. Чтобы свести это к нулю, канал DR должен передавать по крайней мере с такой же скоростью. 3. Канал С Е должен нести 20 бит/сек, следовательно, канал С R должен нести по крайней мере столько же. 4. Канал RT должен нести 2 бит/сек, чтобы нейтрализовать D (из упр. 2), и 20 бит/сек от С; поскольку эти два источника независимы (значения D и С не связаны), пропускная способность канала R Т должна быть самое меньшее 22 бит/сек.

12/8:

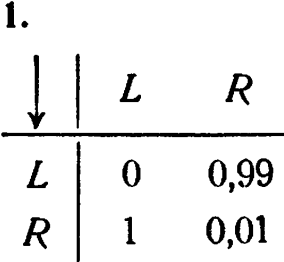
2. Системы почти изоморфны; однако иногда будет прямо перескакивать из А в D, а иногда оставаться на один шаг в С. 3. Последовательные вероятности для а на каждом шаге равны 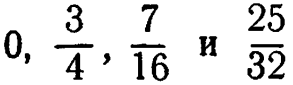вероятности b равны дополнениям этих дробей до единицы. 4. Ответ можно получить, умножая вектор-столбец  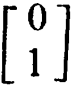на произведение матриц pqr, ср. упр. 2/16/3.    

5. Состояния новой системы должны быть парами, такими, например, как (b, е); поэтому она должна иметь 6 состояний. Теперь найдем вероятности перехода. Чему равна, например, вероятность перехода (b, е) (а, f)? Чтобы это случилось, b должно перейти в а и при этом другая составляющая должна находиться в состоянии е, т. е. в состоянии . Когда вход первой составляющей равен , вероятность ba равна 0,9. Аналогично при состоянии b (т. е. при ) вероятность ef равна 0,3; следовательно, вероятность всего перехода (для чего должны совершиться оба этих независимых события) равна 0,27.

Остальные вероятности находятся совершенно так же, и искомая матрица будет иметь вид (скобки опущены для краткости)

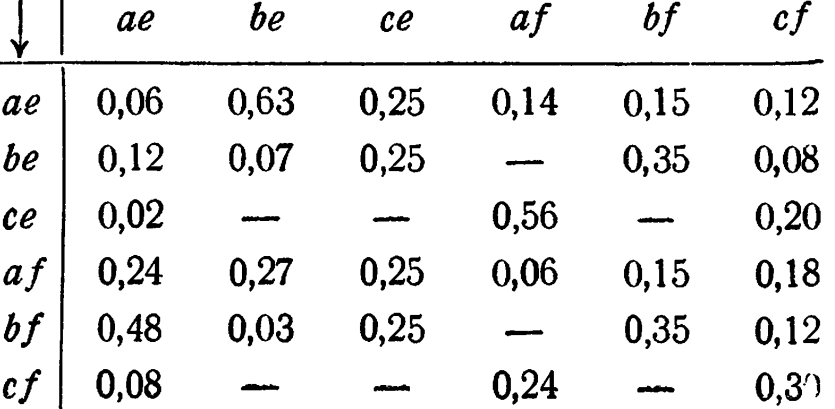
6. Да.

12/10: 1. Возможна, например, такая матрица:

12/11: 1. Только G. 2."Находясь в а или b, она, по-видимому, не знает, где она находится, и блуждает наугад; единственным отличным от а и b отделением, в которое она может пройти из А или В, является отделение с; попав в с, она, по-видимому, узнаёт, где она находится, ибо всегда бежит, не отклоняясь, через d и е в f, где и останавливается, - возможно, ее всегда там кормили".

12/12: 1. (I) Да;

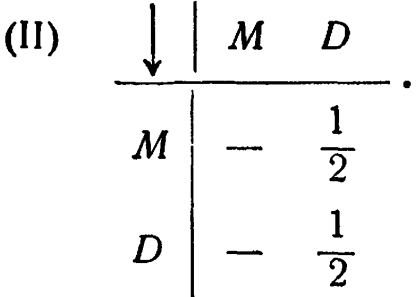Из В нет переходов.

2. Да - для многих существенных переменных!

12/14: 1. должна быть единичной; в на главной диагонали не должно быть 1.

12/17:  

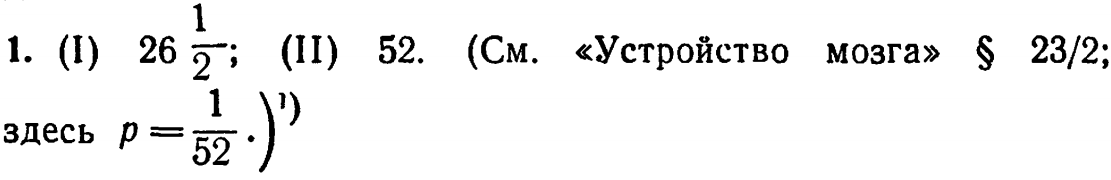
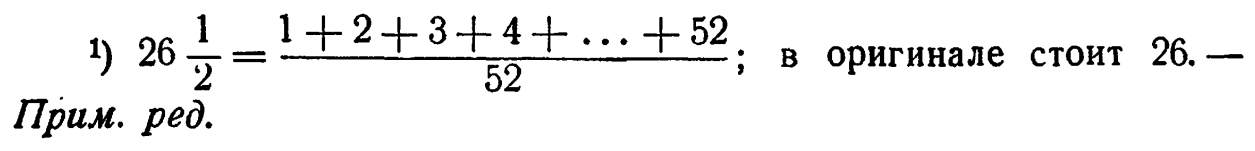
12/21: 1. Две; положения бруса G полностью определяются положениями столба Р, который имеет одну степень свободы; угол поворота рычага J дает вторую. 2. Один из способов - поставить V посредине между L и К. 3. Один из способов - изменить направление движения воздуха, так чтобы он не выходил в V, а входил в него.

13/15: 1. 3log27, т. е. 8,42 бита. 2. 3log291, т. е. 19,52 бита. 3. Минимум 3,3 бита, ибо только 10 комбинаций различны. 4. 1 бит; число состояний и другие подробности не имеют значения. Чтобы понять, что ответ должен быть <1 бит>, представьте себе, что наши две машины - единственно возможные (как это и дано), а затем представьте себе, что проектировщик должен послать свои указания по телеграфу; ясно, что ему не придется платить много, ибо простого различия в 1 бит достаточно, чтобы адресат получил все необходимые указания. 5. (I) 49 800 битов; (II) 1,6 бита; никакого соответствия и нельзя ожидать, ибо эти два значения относятся не к одному штампу, а к двум различным множествам возможностей. 6. nlog2n битов. 7. in log2n битов.

13/17:1. Устраняется 19 возможностей. 2. Устраняется 26 возможностей. 3. 4,75 бита уменьшились до 3,00 бита, так чтй было устранено 1,75 бита. 4. Поскольку a1 может перейти в любое из n - 1 состояний, как и а2, то новое число преобразований равно (n - 1) (n - 1) ... (n - 1) (n раз),т. е. . Логарифмически разнообразие было равно nlog2n, а теперь оно равно nlog2(n - 1), так что разнообразие, устраненное ограничением, равно nlog2n - nlog2(n - 1).

5.     1,4 бита; точнее, оно равно (1 + 1/2n + ...) log2е.

6. Просмотр k-й карты в колоде из n карт дает информацию (или имеет энтропию) 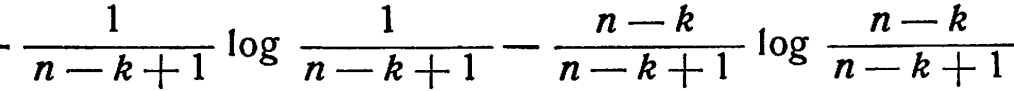, если карта вытаскивается. Если успех достигнут раньше, энтропия равна 0. Вероятности этих двух событий (и их энтропий) равны (n - k +1)/n и (k-1)/n следовательно, взвешенная средняя энтропия равна

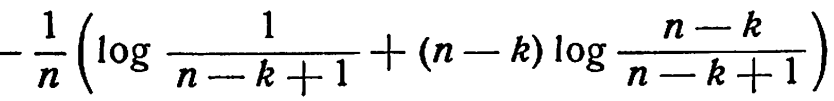
или

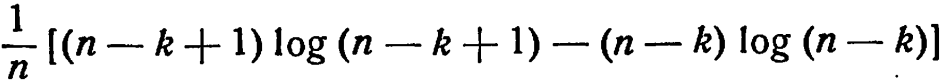
7. При каждом просмотре энтропия одинакова: она равна энтропии вероятностей 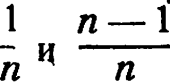 ; отсюда средняя информация равна

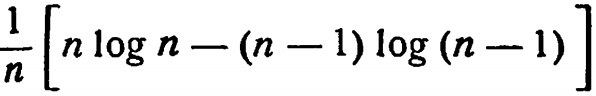
14/1: 1. Конечно, необходим дополнительный вход с достаточным обилием воды. Выход идет от него через край, управляемый основным входом. Один из возможных способов - использовать поршень или мехи, с тем чтобы давление воды, проходящей через узкое отверстие в количестве 0,1 или 2 мл/сек, ставило кран в нужное положение.